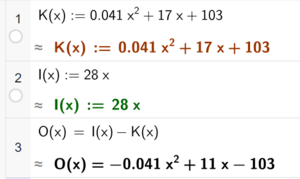S1 2023 Høst LØSNING
Diskusjon av oppgaven på matteprat
Løysingsforslag laga av Torodd F. Ottestad
Løsningsforslag laget av Realfagsportalen
Løsningsforslag laget av Farhan Omar
Videoløsning del 1 av Lektor Lainz (Reabel)
DEL 1
Oppgave 1
Oppgave 2
Vi vet at lg(70) er mellom 1 og 2 fordi lg(10) = 1 og lg(100) = 2. Derfor er 3lg(70) mellom 3 og 6 (større enn 3 og mindre enn 6).
I stigende rekkefølge:
Oppgave 3
a)
P( alle terningen viser forskjellige øyner) =
b)
Sannsynligheten for at nøyaktig to terninger viser samme antall øyne, er alle muligheter minus sannnsynligheten for at alle terningene viser forskjellig antall øyne (funnet oppgave a), og minus sannsynligheten for at alle tre terningene viser samme antall øyne.
Finner først sannsynligheten for at alle terningene viser samme antall øyne: P(alle like øyne) =
P(Kun to terninger viser det samme antall øyner) =
Oppgave 4
For at funksjonen skal være kontinuerlig må funksjonsverdien bli null når x går mot en nedenfra. Dvs.
Oppgave 5
Programmet finner hvor mange enheter som må produseres for at grensekostnaden skal bli lik 200 kroner. Det vil si det antallet enheter som må produseres, for at det skal koste 200 kr å produsere én til.
Setter K'(x)=200
Resultatet er at det må produseres 500 enheter for at grensekostnaden skal være 200 kroner.
DEL 2
Oppgave 1
a)
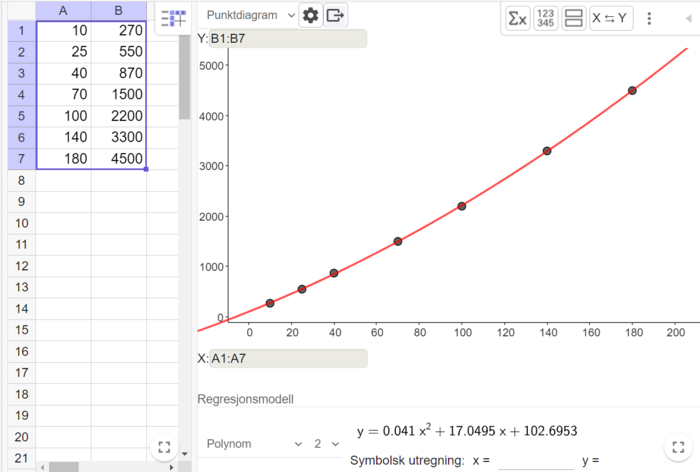
Bruker regresjonsanalyse i Geogebra til å finne et andregradsuttrykk for produksjonskostnaden.
Bruker CAS til å definere kostnadsfunksjonen K(x) (fra regresjonsanalysen), inntektsfunksjonen I(x) (i tusen kroner), og til slutt overskuddsfunksjonen O(x). O(x) er slik det skulle vises.
b)
Bruker CAS til å finne toppunktet i overskuddsfunksjonen. Oppgaven kan også løses grafisk.
En produksjon på 134 sofaer gir størst overskudd per måned.