2P 2024 Vår LØSNING
Diskusjon av oppgaven på matteprat
Løysing laga av Torodd F. Ottestad
DEL 1
Oppgave 1
Gjennomsnitt: legger sammen alle tallene og deler på antall tall.
$\frac{1+ 3+ 4+ 0+ 4+ 5+ 2+ 7+ 12+ 2}{10}=\frac{40}{10}=4$
Gjennomsnittet er 4 timer på sosiale medier per dag.
Median: ordner tallene i stigende rekkefølge og finner gjennomsnittet av de to midterste tallene.
$0, 1, 2, 2, 3, 4, 4, 5, 7, 12$
De to midterste tallene er 3 og 4, og gjennomsnittet av disse er 3,5.
Medianen er 3,5 timer på sosiale medier per dag.
Oppgave 2
Prisen på varen følger konsumprisindeksen. Dersom varen kostet 1000 kr i 2015, ville den kostet 1296 kr i 2023. Siden varen kostet 500 kr i 2015 (altså halvparten av 1000), vil varen koste 648 kr (halvparten av 1296 kr) i 2023.
Oppgave 3
Målestokk angir hvor mange cm i virkeligheten én cm på kartet viser.
2 cm på Astrids kart tilsvarer 300 m i virkeligheten, som vil si at 1 cm på Astrids kart tilsvarer 150 m i virkeligheten.
150 m = 15 000 cm, altså er målestokken 1:15000.
Oppgave 4
x = pris for én ispinne
y = pris for én boks med mineralvann
Lager et likningssystem:
Likning I $\quad 30x+30y=900$
Likning II $\quad y=x+6$
Bruker innsettingsmetoden og setter inn verdien for y fra likning II, inn i likning I.
$30x+30(x+6)=900$
$30x+30x+180=900$
$60x=900-180$
$x=\frac{720}{60}$
$x = 12$
Setter inn verdien for x inn i likning II:
$y = x+6$
$y = 12+6= 18$
En ispinne kostet 12 kroner, og en boks med mineralvann kostet 18 kroner.
Oppgave 5
Pris per bagett i det første tilbudet: 32 kr / 2 = 16 kr
Pris per bagett i det andre tilbudet: 48 kr / 4 = 12 kr
Prisforskjell per bagett: 16 kr - 12 kr = 4 kr
Prosent forskjell i pris per bagett, sammenlignet med den dyreste prisen: $\frac{4}{16}\cdot 100\%=\frac{1}{4}\cdot 100\%=25\%$
Det blir 25 % billigere per bagett å kjøpe fire bagetter, enn å kjøpe to bagetter.
DEL 2
Oppgave 1
a)
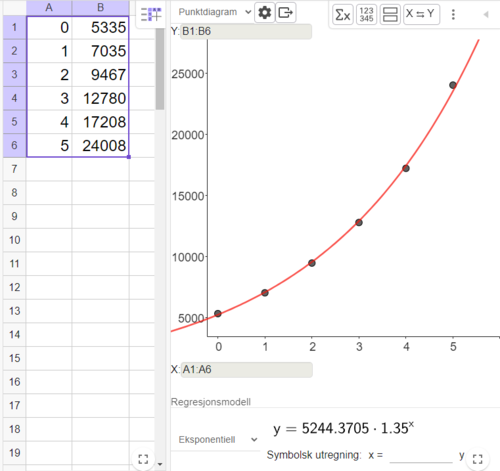
Tuva kan ha brukt eksponentiell regresjonsanalyse, som vist under i Geogebra.
I modellen $f(x)=5244\cdot1,35^x$ vekstfaktoren 1,35, som betyr en månedlig vekst på 35 % følgere.
b)
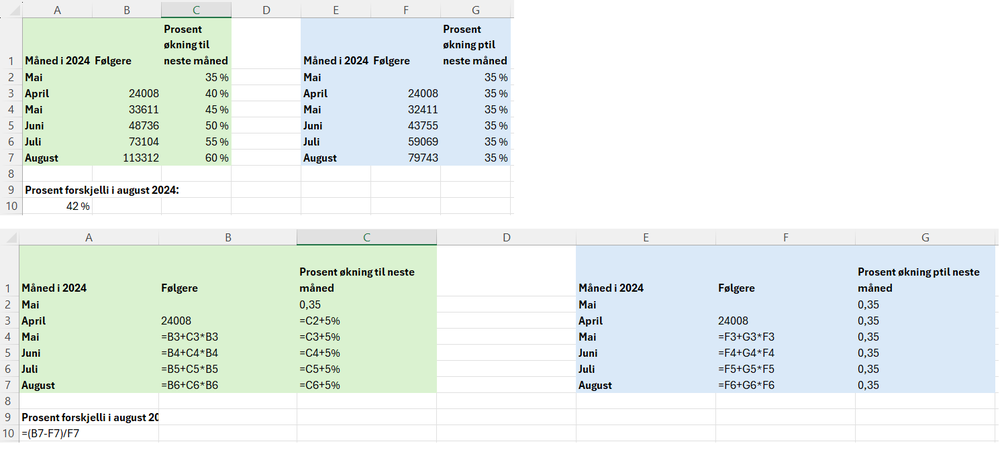
Jeg forstår spørsmålet som at antall følgere skal øke med 40 % fra april til mai, og med 45 % fra mai til juni.
Antall følgere i mai: $24008\cdot 1,40 \approx 33611$
Antall følgere i juni: $33611\cdot 1,45 \approx 48736$
c)
Jeg løser oppgaven i Excel.
Tuva vil ha 42 % prosent flere følgere i august 2024 dersom hun klarer å nå det nye målet sitt for hver måned, sammenliknet med om økningen fortsetter å være på 35 % hver måned.
Oppgave 2
a)
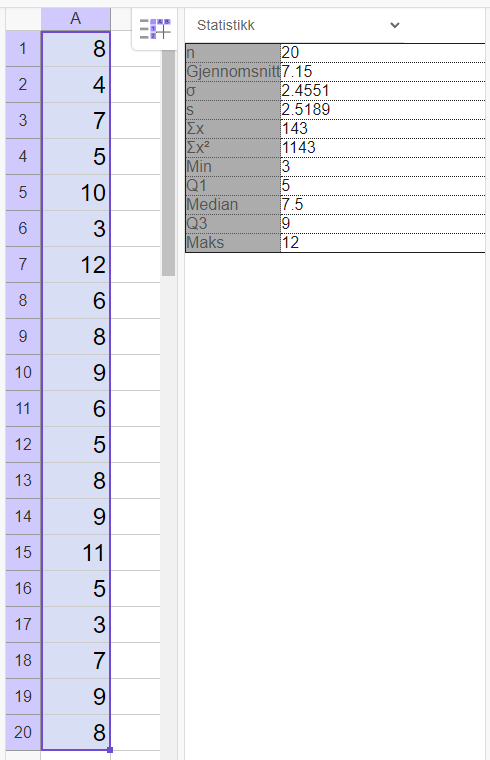
Bruker Geogebra til å finne statistikk for Solveigs skiturer:
I gjennomsnitt brukte Solveig 7,15 timer per skitur, mens Miriam brukte 4,7 timer per skitur. Gjennomsnittlig varte altså skiturene til Solveig lengre.
Medianen for Solveigs skiturer var 7,5 timer, mot 4 timer for Miriam. Det vil si at halvparten av skiturene til Solveig varte mer enn 7,5 timer, mens halvparten av skiturene til Miriam varte mer enn 4 timer.
Standardavviket for Solveigs skiturer er ca. 2,5 timer, med for Miriam er det 4,2. Det vil si at Miriam har større variasjon i varigheten på skiturene. Hun kan ha hatt noen veldig korte og noen veldig lange skiturer. Solveig holder seg nærmere gjennomsnittsvarigheten på sine skiturer.
Miriam har et gjennomsnitt som er høyere enn medianen, som vil si at hun har en eller flere lange skiturer som "drar opp" gjennomsnittet.
Solveig har et gjennomsnitt som er lavere enn medianen, som vil si at hun har en eller flere korte skiturer som "drar ned" gjennomsnittet.
b)
1) I den andre raden i tabellen står det at jentene gikk 11 skiturer på 3 timer eller mindre. I den tredje raden i tabellen står det at jentene gikk 14 skiturer på 5 timer eller mindre. Det må bety at 3 av skiturene var på 5 timer.
2) Vi ser av tallene over oppgave a) at Solveig gikk fire skiturer på 8 timer. Tabellen i oppgave b) viser at jentene bare gikk tre skiturer på 8 timer sammen. Det vil si at Miriam ikke var med på én av 8-timers turene til Solveig.
Oppgave 3
Påstand 1: "80 elever brukte mindre enn 40 minutter på lekser denne ettermiddagen."
Vi ser på første søyle i histogrammet, og ganger klassebredden med høyden på søylen: $40 \cdot 2 = 80$. Dette gir oss en frekvens på 80 stykker i klassen 0-40 minutter med lekser. Påstanden er riktig.
Påstand 2: "Den relative frekvensen for 100–150 minutter brukt på lekser er 1/5."
Vi finner frekvensen for alle søylene til sammen: $40\cdot 2 + 20\cdot 6 + 40\cdot 5 + 50\cdot 2 = 80+120+200+100 = 500$
Frekvensen for klassen 100-150 minutter er 100.
Den relative frekvensen for klassen 100-150 minutter er da 100 / 500 = 1/5. Påstanden er riktig.
Påstand 3: "Elevene som brukte mindre enn 60 minutter på leksene, brukte i gjennomsnitt 38 minutter."
80 elever brukte 0-40 minutter (gjennomsnittlig 20 minutter) og 120 elever brukte 40-60 minutter (gjennomsnittlig 50 minutter) på lekser.
$\frac{80\cdot 20 + 120\cdot 50}{200} = \frac{7600\, min}{200\, elever}=38 \, min/elev$. Påstanden er riktig.
Påstand 4: "For elevene som brukte mindre enn 60 minutter på leksene, er medianen for antall minutter høyere enn gjennomsnittet for antall minutter."
80 elever brukte 0-40 minutter og 120 elever brukte 40-60 minutter på lekser. Det er 200 elever til sammen i disse to klassene, og det betyr at medianelevene nr. 100 og 101 er i klassen 40-60 minutter. Medianen er altså mer enn gjennomsnittet (38 minutter). Påstanden er riktig.
Oppgave 4
a)
Sara har først omformet likningene til å være uttrykt ved y (før hun laget programmet). I programmet definerer hun likningene som funksjoner f(x) og g(x) i linje 1-2 og 4-5.
Deretter lager Sara en for-løkke som går gjennom alle x-verdier (hele tall) fra og med -5 til 5 (det vil si til og med 4), og tester med en if-setning om funksjonene f(x) og g(x) har lik funksjonsverdi for hver av disse x-verdiene. Dersom funksjonsverdiene er like, skrives x- og y-verdien ut. Programmet til Sara er en slags "prøve-og-feile" metode.
b)
Ole må omforme sine likninger til å være uttrykt med y, og bruke disse i definisjonen av f(x) og g(x). Jeg brukte CAS til å løse likningssystemet, og fikk løsninger når x=-7 og x=8, så Ole må endre for-løkka til gå fra og med -7 til 9, slik at løsningsverdiene er med i løkka.
Oppgave 5
a)
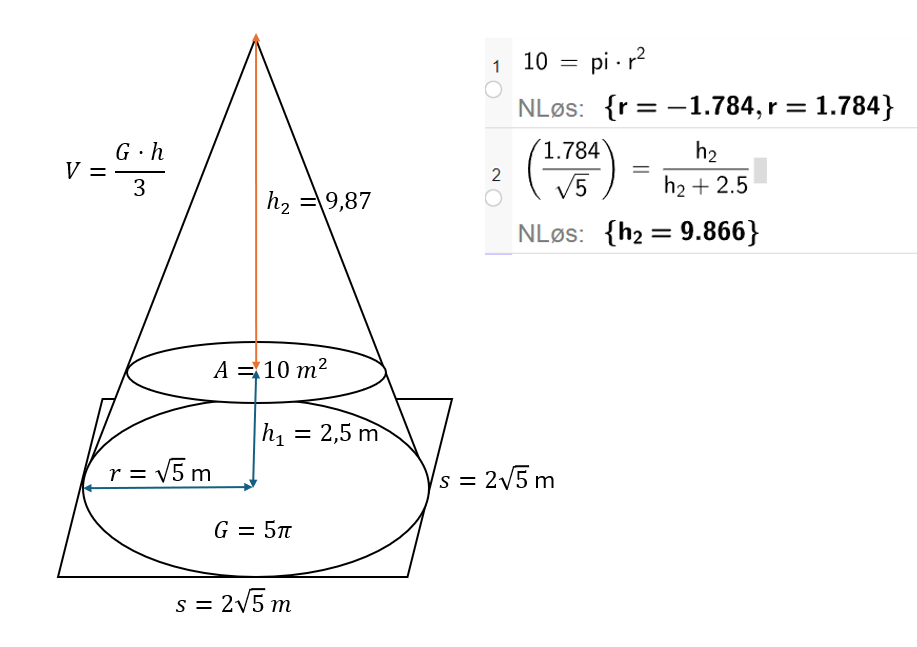
Siden arealet til kvadratet som klatreveggen skal bygges på er $20\,m^2$, er sidelengden $\sqrt{20}\,m=2\sqrt{5}\,m$. Det betyr at diameter til grunnflaten til kjeglen må være maksimum $2\sqrt{5}\,m$ , og radius er da maksimum $\sqrt{5}\,m$ .
Arealet til kjeglens grunnflate er da: $G=\pi \cdot r^2=\pi\cdot\sqrt{5\,m}^2=5\pi\,m^2$
For å finne høyden i den øverste kjeglen (h2), finner jeg først radius i grunnflaten til den øverste kjeglen, og bruker deretter formlikhet, se utklippet fra CAS til høyre i bildet.
b)
Bruker CAS i Geoegbra. Finner først hele høyden til den største kjegla (linje 3), volum til hele kjegla (linje 4), så volum til den øverste kjegla (linje 4), og til slutt volum til selve klatreveggen (linje 5).
Det går med ca. $32\,m^3$ betong for å lage klatreveggen.
Oppgave 6
a)
Jeg kan se at det er et annuitetslån fordi det er samme lånekostnad per måned.
Johannes kan ikke låne mer enn 1 700 000 kr når boligens pris er 2 000 000 kr, fordi han må ha minst 15 % i egenkapital. 15 % av 2 000 000 kr er 300 000 kr.
b)
Utregningen regner ut vekstfaktor for én måned (1+0,015) og ganger deretter denne vekstfaktoren med seg selv 12 ganger, for å få total vekstfaktor i løpet av et år. Vekstfaktoren for hele året er 1,1956, som vi si en rente på 19,56 % per år.
Jeg kan bruke CAS i Geogebra for å finne Johannes sin månedlige rente:
Johannes sin årlige rente på 5,49 % tilsvarer en månedlig rente på 0,446 %.