2P 2024 Vår LØSNING
Diskusjon av oppgaven på matteprat
Løysing laga av Torodd F. Ottestad
DEL 1
Oppgave 1
Gjennomsnitt: legger sammen alle tallene og deler på antall tall.
$\frac{1+ 3+ 4+ 0+ 4+ 5+ 2+ 7+ 12+ 2}{10}=\frac{40}{10}=4$
Gjennomsnittet er 4 timer på sosiale medier per dag.
Median: ordner tallene i stigende rekkefølge og finner gjennomsnittet av de to midterste tallene.
$0, 1, 2, 2, 3, 4, 4, 5, 7, 12$
De to midterste tallene er 3 og 4, og gjennomsnittet av disse er 3,5.
Medianen er 3,5 timer på sosiale medier per dag.
Oppgave 2
Prisen på varen følger konsumprisindeksen. Dersom varen kostet 1000 kr i 2015, ville den kostet 1296 kr i 2023. Siden varen kostet 500 kr i 2015 (altså halvparten av 1000), vil varen koste 648 kr (halvparten av 1296 kr) i 2023.
Oppgave 3
Målestokk angir hvor mange cm i virkeligheten én cm på kartet viser.
2 cm på Astrids kart tilsvarer 300 m i virkeligheten, som vil si at 1 cm på Astrids kart tilsvarer 150 m i virkeligheten.
150 m = 15 000 cm, altså er målestokken 1:15000.
Oppgave 4
x = pris for én ispinne
y = pris for én boks med mineralvann
Lager et likningssystem:
Likning I $\quad 30x+30y=900$
Likning II $\quad y=x+6$
Bruker innsettingsmetoden og setter inn verdien for y fra likning II, inn i likning I.
$30x+30(x+6)=900$
$30x+30x+180=900$
$60x=900-180$
$x=\frac{720}{60}$
$x = 12$
Setter inn verdien for x inn i likning II:
$y = x+6$
$y = 12+6= 18$
En ispinne kostet 12 kroner, og en boks med mineralvann kostet 18 kroner.
Oppgave 5
Pris per bagett i det første tilbudet: 32 kr / 2 = 16 kr
Pris per bagett i det andre tilbudet: 48 kr / 4 = 12 kr
Prisforskjell per bagett: 16 kr - 12 kr = 4 kr
Prosent forskjell i pris per bagett, sammenlignet med den dyreste prisen: $\frac{4}{16}\cdot 100\%=\frac{1}{4}\cdot 100\%=25\%$
Det blir 25 % billigere per bagett å kjøpe fire bagetter, enn å kjøpe to bagetter.
DEL 2
Oppgave 1
a)
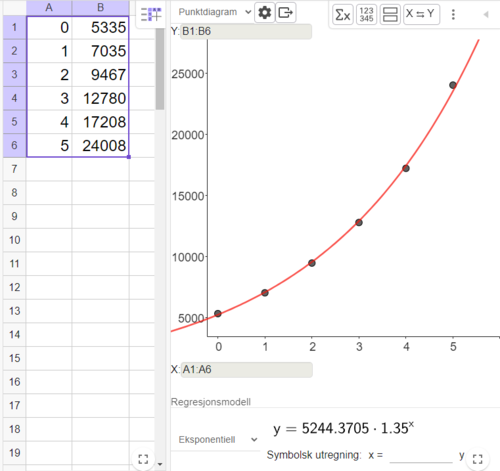
Tuva kan ha brukt eksponentiell regresjonsanalyse, som vist under i Geogebra.
I modellen $f(x)=5244\cdot1,35^x$ vekstfaktoren 1,35, som betyr en månedlig vekst på 35 % følgere.
b)
Jeg forstår spørsmålet som at antall følgere skal øke med 40 % fra april til mai, og med 45 % fra mai til juni.
Antall følgere i mai: $24008\cdot 1,40 \approx 33611$
Antall følgere i juni: $33611\cdot 1,45 \approx 48736$
c)
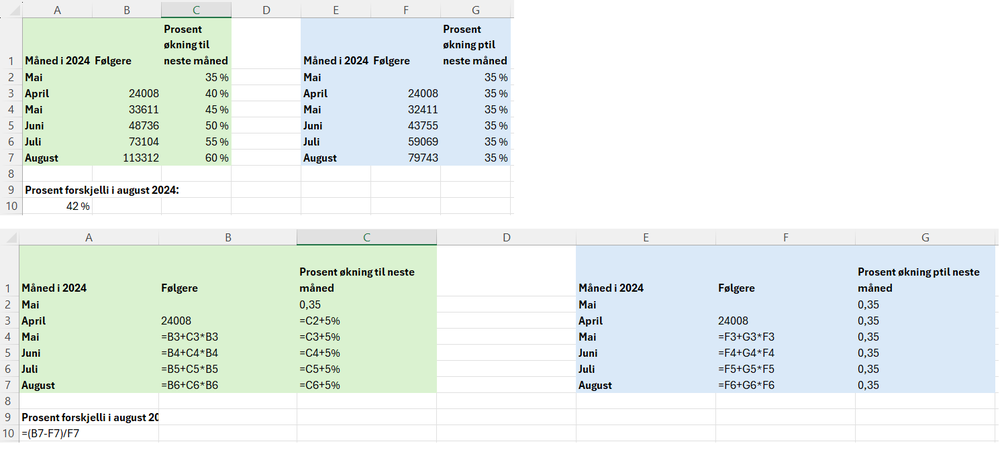
Jeg løser oppgaven i Excel.
Tuva vil ha 42 % prosent flere følgere i august 2024 dersom hun klarer å nå det nye målet sitt for hver måned, sammenliknet med om økningen fortsetter å være på 35 % hver måned.
Oppgave 2
a)
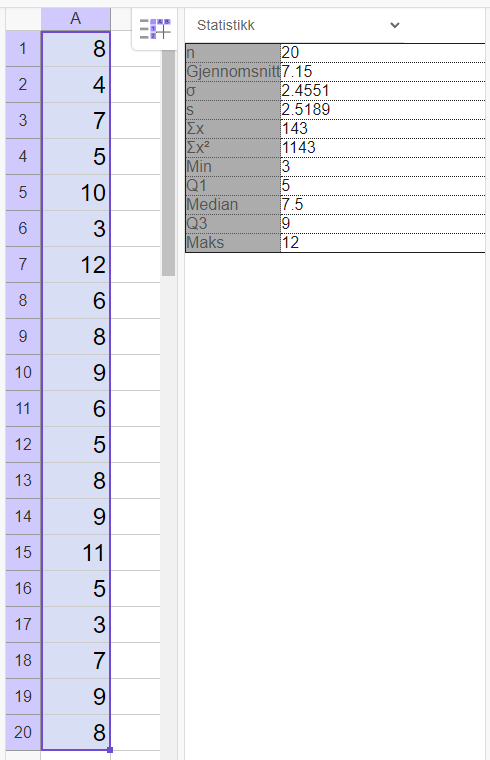
Bruker Geogebra til å finne statistikk for Solveigs skiturer:
I gjennomsnitt brukte Solveig 7,15 timer per skitur, mens Miriam brukte 4,7 timer per skitur. Gjennomsnittlig varte altså skiturene til Solveig lengre.
Medianen for Solveigs skiturer var 7,5 timer, mot 4 timer for Miriam. Det vil si at halvparten av skiturene til Solveig varte mer enn 7,5 timer, mens halvparten av skiturene til Miriam varte mer enn 4 timer.
Standardavviket for Solveigs skiturer er ca. 2,5 timer, med for Miriam er det 4,2. Det vil si at Miriam har større variasjon i varigheten på skiturene. Hun kan ha hatt noen veldig korte og noen veldig lange skiturer. Solveig holder seg nærmere gjennomsnittsvarigheten på sine skiturer.
b)
1) I den andre raden i tabellen står det at jentene gikk 11 skiturer på 3 timer eller mindre. I den tredje raden i tabellen står det at jentene gikk 14 skiturer på 5 timer eller mindre. Det må bety at 3 av skiturene var på 5 timer.
2) Vi ser av tallene over oppgave a) at Solveig gikk fire skiturer på 8 timer. Tabellen i oppgave b) viser at jentene bare gikk tre skiturer på 8 timer sammen. Det vil si at Miriam ikke var med på én av 8-timers turene til Solveig.
Oppgave 3
Påstand 1: "80 elever brukte mindre enn 40 minutter på lekser denne ettermiddagen."
Vi ser på første søyle i histogrammet, og ganger klassebredden med høyden på søylen: $40 \cdot 2 = 80$. Dette gir oss en frekvens på 80 stykker i klassen 0-40 minutter med lekser. Påstanden er riktig.
Påstand 2: "Den relative frekvensen for 100–150 minutter brukt på lekser er 1/5."
Vi finner frekvensen for alle søylene til sammen: $40\cdot 2 + 20\cdot 6 + 40\cdot 5 + 50\cdot 2 = 80+120+200+100 = 500$
Frekvensen for klassen 100-150 minutter er 100.
Den relative frekvensen for klassen 100-150 minutter er da 100 / 500 = 1/5. Påstanden er riktig.
Påstand 3: "Elevene som brukte mindre enn 60 minutter på leksene, brukte i gjennomsnitt 38 minutter."
80 elever brukte 0-40 minutter (gjennomsnittlig 20 minutter) og 120 elever brukte 40-60 minutter (gjennomsnittlig 50 minutter) på lekser.
$\frac{80\cdot 20 + 120\cdot 50}{200} = \frac{7600\, min}{200\, elever}=38 \, min/elev$. Påstanden er riktig.
Påstand 4: "For elevene som brukte mindre enn 60 minutter på leksene, er medianen for antall minutter høyere enn gjennomsnittet for antall minutter."
80 elever brukte 0-40 minutter og 120 elever brukte 40-60 minutter på lekser. Det er 200 elever til sammen i disse to klassene, og det betyr at medianelevene nr. 100 og 101 er i klassen 40-60 minutter. Medianen er altså mer enn gjennomsnittet (38 minutter).