Statistikk I
Innledning
Statistikk er å bearbeide tallmaterialet / data slik at man forhåpentligvis kan observere en trend eller tendens. I beste fall kan man trekke en konklusjon. Tallmaterialet skaffes ofte ved hjelp av spørreundersøkelser, målinger eller observasjoner. Statistikk kan presenteres i forskjellige former og det kan være en god måte å speile virkeligheten på. Statistikk kan også, uten å være direkte feil, presenteres på en måte som tåkelegger virkeligheten. I slike tilfeller er det ofte interessegrupper som presenterer et tallmaterialet med det formål å fremme sin sak. VÆR PÅ VAKT, i slike tilfeller er statistikk mer forvirrende en forklarende.
Frekvenstabell
Eksempel
En liten skoleklasse har femten elever. Høyden på elevene målt i cm. er slik:
178, 142, 156, 162, 154 , 156, 163, 169, 172, 142, 156, 172, 173, 161, 169
Vi kan sette resultatet opp i en tabell
Høyde x 142 154 156 161 162 163 169 172 173 178 Frekvens f 2 1 3 1 1 1 2 2 1 1 N = 15 N er antall målinger, i dette tilfellet antall elever. Man ser at frekvensen er 3 for høyden 156 cm.
Søylediagram
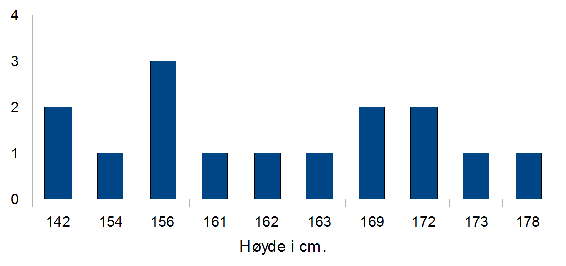
Med frekvens mener vi hvor mange ganger en verdi forekommer. Tabellen kan presenteres som den er, eller vi kan presentere den som et diagram. Et eksempel kan være et søylediagram. På y aksen har vi antall observasjoner og på x aksen har vi de forskjellige type observasjoner.
På y aksen har man antall eller frekvens, og på x aksen høyden
Gjennomsnitt
Gjennomsnitt er summen av alle verdier delt på antall verdier.
| Høyde x | Frekvens f | Sum høyde f <tex> \cdot </tex> x |
| 142 | 2 | 2 <tex> \cdot </tex> 142 |
| 154 | 1 | 154 |
| 156 | 3 | 3 <tex>\cdot </tex> 156 |
| 161 | 1 | 161 |
| 162 | 1 | 162 |
| 163 | 1 | 163 |
| 169 | 2 | 2<tex>\cdot </tex> 169 |
| 172 | 2 | 2<tex>\cdot </tex> 172 |
| 173 | 1 | 173 |
| 178 | 1 | 178 |
| N = 15 | S = 2425 |
Gjennomsnittet er summen av alle høydene delt på antall elever:
Gjennomsnitt: <tex> \frac SN= \frac{2425 cm}{15}= 161,7cm</tex>
Median
Median er den midterste verdien etter alle verdien er blitt sortert i stigende rekkefølge.
Fra eksemplet over har man: (142, 142, 154, 156, 156, 156, 161,162, 163, 169, 169, 172, 172, 173, 178). 162 er det tallet som står midt i rekka når verdiene er sortert i stigende rekkefølge og derved median.
Dersom antall observasjoner er partall vil to tall stå i midten. Median blir da gjennomsnittet av disse.
Typetall
Typetallet er den verdi som det er flest forekomster av i datamengden. I eksempelet over er typetallet 156 cm, fordi det forekommer flest (3) ganger.
Dersom flere verdier skulle opptre i like antall og disse har høyeste frekvens, må alle oppgies som typetall.
Spredningsmål
Median
Median er midt i tallmaterialet. Det betyr at 50% av tallmaterialet er mindre enn median, og 50% er større.
Nedre kvartil
Dersom man tar den nedre halvpart av tallmaterialet og deler den i to, vil "midtpunktet" av denne delen kalles nerdre kvartil, eller 25% prosenttilet.
Dersom man ser på måling av høyden på elevene i skoleklassen er nedre halvdel disse høydene: 142, 142, 154, 156, 156, 156, 161
Den midterste verdien er 156, som da er nedre kvartil.
Øvre kvartil
Dersom man tar den øvre halvpart av tallmaterialet og deler den i to, vil "midtpunktet" av denne delen kalles øvre kvartil, eller 75% prosenttilet.
Dersom man ser på måling av høyden på elevene i skoleklassen er øvre halvdel disse høydene:163, 169, 169, 172, 172, 173, 178.
Den midterste verdien er 172, som da er øvre kvartil.
Kvartilbredde
Kvartilbredden er differansen mellom øvre og nedre kvartil. Kvartilbredden vil inneholde halvparten av måledataene i måleserien.
I eksempelet med høyden på elevene i klassen er kvartilbredden:
Kvartilbredde = 172cm - 156cm = 16cm
Det betyr at halvparten av eleven har en høyde som ligger innefor en forskjell på 16cm.
Varians
Gjennomsnittet av høydemålingene over var 161,7cm. Man sammenligner hver enkel måling opp mot gjennomsnittet på den måten at man finner avviket og kvadrerer dette. Man får:
| Høyde x | (gjennomsnitt - måling) <tex>^2 </tex> |
| 142 | (161,7 - 142)<tex>^2 </tex> = 19,7<tex>^2 </tex> = 388,1 |
| 142 | (161,7 - 142)<tex>^2 </tex> = 19,7<tex>^2 </tex> = 388,1 |
| 154 | (161,7 - 154)<tex>^2 </tex> = 7,7<tex>^2 </tex> = 59,3 |
| 156 | (161,7 - 156)<tex>^2 </tex> = 5,7<tex>^2 </tex> = 32,5 |
| 156 | (161,7 - 156)<tex>^2 </tex> = 5,7<tex>^2 </tex> = 32,5 |
| 156 | (161,7 - 156)<tex>^2 </tex> = 5,7<tex>^2 </tex> = 32,5 |
| 161 | (161,7 - 161)<tex>^2 </tex> = 0,7<tex>^2 </tex> = 0,5 |
| 162 | (161,7 - 162)<tex>^2 </tex> = (-0,3)<tex>^2 </tex> = 0,1 |
| 163 | (161,7 - 163)<tex>^2 </tex> = (-1,3)<tex>^2 </tex> = 1,7 |
| 169 | (161,7 - 169)<tex>^2 </tex> = (-7,3)<tex>^2 </tex> = 53,3 |
| 169 | (161,7 - 169)<tex>^2 </tex> = (-7,3)<tex>^2 </tex> = 53,3 |
| 172 | (161,7 - 172)<tex>^2 </tex> = (-10,3)<tex>^2 </tex> = 106,1 |
| 172 | (161,7 - 172)<tex>^2 </tex> = (-10,3)<tex>^2 </tex> = 106,1 |
| 173 | (161,7 - 173)<tex>^2 </tex> = (-11,3)<tex>^2 </tex> = 127,7 |
| 178 | (161,7 - 178)<tex>^2 </tex> = (-16,3)<tex>^2 </tex> = 265,7 |
| SUM = 1647,5 |
Når man deler summen av kvadratene på antall målinger får man variansen: <tex>Var = \frac{Sum}{N} = \frac{1647,5}{15} = 109,8 </tex>
Standardavik
Standardavviket er et mål på spredningen rundt gjennomsnittet. Standardavviket er kvadratroten av variansen: Standardavvik = <tex> \sqr{Var} = \sqr{109,8} = 10,5</tex>
Boksplott
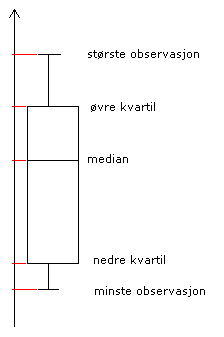
For å angi typeske verdier for et utvalg kan man oppgi gjennomsnitt, median eller typetall. Dersom fordelingen i utvalget er skjev kan det være store forskjeller på de tre størrelsene. For at leseren skal få mest mulig informasjon må det framgå hvilket sentralmål som brukes (bruk gjerne flere). Alternativt kan man lage et boksplott:
Median er det samme som 50 - prosenttilet, det betyr at 50% av observasjonene er mindre enn median. Tilsvarende er 25% av observasjonene mindre enn nedre kvartil (25 - prosenttilet) og 75% av observasjonene mindre enn øvre kvartil (75 - prosenttilet).
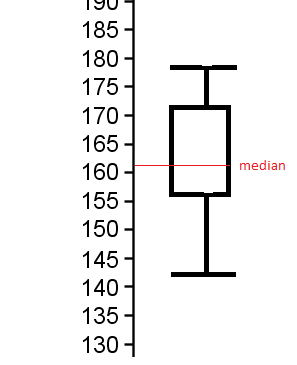
I eksempelet med høyden på elevene i klassen ser boksplottet slik ut:
Man merker seg at det er informasjon om median, nedre og øvre kvartil, samt største og minste observasjon, i samme grafiske fremstilling.
histogram
Det er ikke altid praktisk å behandle hver observasjonsverdi individuelt. Dersom vi måler høyden på alle eleven på en 1 - 10 skole med 556 elever er det upraktisk å behandle alle høyder individuelt fordi høydene vil sprike mye og datamengden er stor.
Dette løses ved å dele tallmaterialet opp i grupper. Man kan for eksempel gruppere slik:
| Klasse [a,b>, Høyde på elever |
Frekvens f | Klassebredde b-a | Høyde på histogram <tex> \frac{f}{b-a} </tex> |
| Klasse [130,140> | 18 | 10 | 1,8 |
| Klasse [140,150> | 29 | 10 | 2,9 |
| Klasse [150,160> | 102 | 10 | 10,2 |
| Klasse [160,165> | 89 | 5 | 17,8 |
| Klasse [165,170> | 117 | 5 | 23,4 |
| Klasse [170,175> | 122 | 5 | 24,4 |
| Klasse [175, 180> | 67 | 5 | 13,4 |
| Klasse [180,190> | 12 | 10 | 1,2 |
| 556 |
Høyden [130,140> inkluderer alle elever som har høyde fra og med 130cm til 140cm, men ikke 140cm. Høyden 140cm vil ligge i gruppen [140, 150> osv. Intervallene omfatter 10cm og det kalles for klassebredden. Man kan ha søyler med varierende klassebredde i samme histogram, dvs. alle gruppene trenger ikke ha bredden 10cm. Dette materialet er inndelt i åtte klasser.
Søylehøyde <tex> = \frac{frekvens}{klassebredde}</tex>
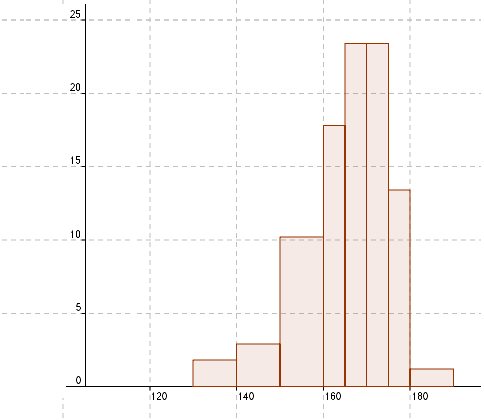
Histigrammet ser slik ut:
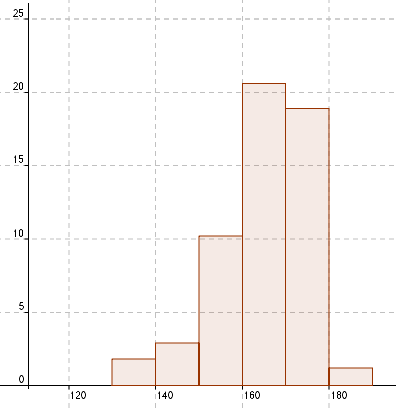
I fremstillingen over har klassene forskjellig bredde. Dersom man holder bredden lik i alle klassene, for eksempel 10 cm. blir resultatet slik:
| Klasse [a,b>, Høyde på elever |
Frekvens f | Klassebredde b-a | Høyde på histogram <tex> \frac{f}{b-a} </tex> |
| Klasse [130,140> | 18 | 10 | 1,8 |
| Klasse [140,150> | 29 | 10 | 2,9 |
| Klasse [150,160> | 102 | 10 | 10,2 |
| Klasse [160,170> | 206 | 10 | 20,6 |
| Klasse [170,180> | 189 | 10 | 18,9 |
| Klasse [180,190> | 12 | 10 | 1,2 |
| 556 |
Det tilhørende histigrammet blir da slik:
Hva er forskjellen på de to histogrammene? Man ønsker at en grafisk fremmstilling skal være lett å lese. Dersom klassebredden blir liten blir diagrammet hakkete og vannskelig å lese. dersom klassebredden blir for stor mister man verdifull informasjon. Dersom klassebredden varierer i et diagram, kan de gi leseren økt informasjon, men det gir også et diagram som er vannskeligere å lese. Ofte ser man at histogrammer har lik klassebredde, gjerne mellom 5 og 15 enheter.
Gjennomsnitt i gruppert materiale
Man finner klassemidtpunktet i de forskjellige klassene. <tex>x_m</tex>
Man multiplisere klassemidtpunktet med antallet i klassen (varierer fra klasse til klasse). og får: <tex>x_m \cdot f</tex>
Man legger sammen <tex>x_m \cdot f</tex> for alle klassene, i eksemplet over var det åtte klasser. Matematisk kan det skrives slik <tex>\sum x_m \cdot f</tex>
<tex>\sum </tex> er et "summetegn" og betyr at man legger sammen alle klassene, alså alle <tex>x_m \cdot f</tex>
Man deler så <tex>\sum x_m \cdot f</tex> med summen av alle frekvkvensene i hver klasse, og får gjennomsnittet:
<tex>\bar{x}=\frac{\sum x_m \cdot f}{\sum f}</tex>
Den gjennomsnittsverdien man får er ikke helt riktig, for den forutsetter en jevn fordeling innen hver klasse, men gir en tilnærmet verdi.
I eksemplet med høyden på elevene ved skolen blir det slik (Her tar man utgangspunkt i den siste klassedelingen der alle klassebreddene var 10cm.):
| Klasse [a,b>, Høyde på elever |
Midtpunkt <tex>x_m</tex> | Frekvens f | <tex> x_m \cdot f</tex> | |
| Klasse [130,140> | 135 | 18 | 2430 | |
| Klasse [140,150> | 145 | 29 | 4205 | |
| Klasse [150,160> | 155 | 102 | 15810 | |
| Klasse [160,170> | 165 | 206 | 33990 | |
| Klasse [170,180> | 175 | 189 | 33075 | |
| Klasse [180,190> | 185 | 12 | 2220 | |
| SUM | 556 | 91730 |
Median i gruppert materiale
For å finne medianen I et gruppert tallmateriale gjør man følgende:
Man regner ut den relative kumulative frekvensen for alle klassene.
Med den relative frekvensen mener man frekvensen i prosent.
Med kumulativ mener man at man samler opp, altså legger sammen prosentene etter hvert som man regner ut den relative frekvens for hver klasse.
Først bør man lage en tabell som likner på denne:
Når man har tabellen plotter man resultatene i et koordinatsystem.