1P 2022 høst LK20 LØSNING

DEL EN

Oppgave 1

Promille er del av 1000 og prosent er del av 100. En prosent (%) er altså 10 promille (‰).

a)

Tre promille av to og en halv million:

$2500000 \cdot \frac{3}{1000} = 2500 \cdot 3 = 7500 $kr.

b)

Økningen er fra 0,3 % til 0,35 %, altså en økning på 0,05 prosentpoeng.

Oppgave 2

De ønsker å bygge: $140 m^2 + (6m \cdot 8m) = 188 m^2$

Reguleringsplanen tillater: $600 m^2 \cdot 0,3 = 180 m^2$

Det er ikke mulig, åtte kvadratmeter for mye.

Oppgave 3

a)

Se nøye på tallene. 4, 25, 49, 81, 100.

Dersom man tar kvadratroten: 2, 5, 7, 9, 10

Grafen kan representere en kvadratrot funksjon: $f(x) = \sqrt{x}$

b)

$f(16)= \sqrt{16} = 4$

$f(400)= \sqrt{400} = 20$

$f( \frac 94)= \sqrt{\frac 94} = \frac 32$

$f(-25)$ er ikke mulig da vi ikke greier å finne to like tall som ganget med hverandre blir - 25. Minus fem ganger minus fem er positiv tjuefem.

Oppgave 4

a)

Stigningstallet:

$a= \frac{y_2-y_1}{x_2-x_1} = \frac{538-159}{142-42}= \frac{379}{100} = 3,79$

Det betyr at en gallon er ca. 3,79 liter.

b)

I liter per dag blir det ca:

$3,79\cdot 42 \cdot 10^8 = 159,18 \cdot 10^8 \approx 1,6 \cdot 10^{10}$

DEL TO

Oppgave 1

a)

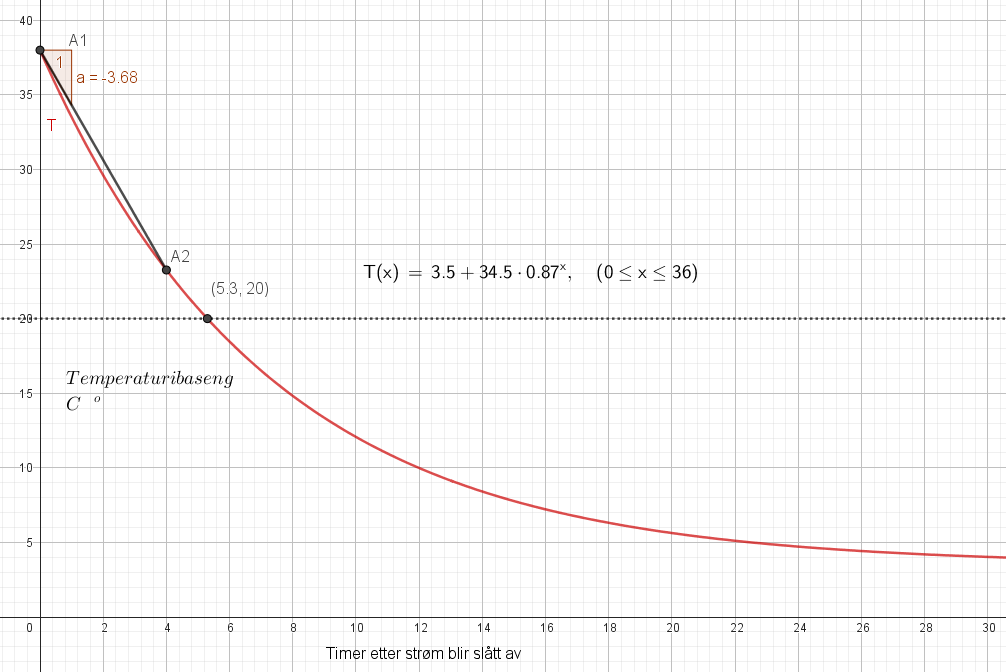
Da er x null, så temperaturen blir da 3,5 + 34,5 = 38 grader celsius når strømmen slåes av.

b)

Det tar ca. 5 timer og 20 minutter.

c)

Den er -3,68 , se figur, Det betyr at temperaturen i bassenget avtar i gjennomsnitt med 3,7 grader per time, de fire første timene etter at strømmen dr skrudd av.

d)

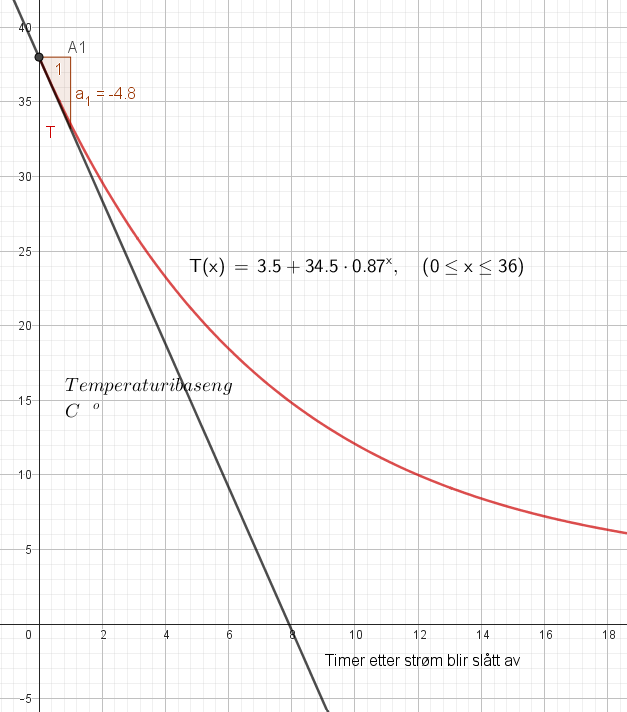
Den mest ekstreme momentane endringen er i starten, rett etter at strømmen blir slått av. Da er endringen - 4,8, Temperaturen synker ikke med mer enn det.

e)

3,5 er omgivelsenes temperatur.

Oppgave 2

Det er 40 leiligheter, og hvis alle var toroms, ville det vært 80 rom til sammen. Siden det er 90 rom til sammen, vet vi da at det er 10 treromsleiligheter. De andre 30 er toromsleiligheter.

Oppgave 3

a)

Kurven har form som tilsier omvendt proporsjonalitet. La oss undersøke nærmere. 60 min er en time. Vi ser at med fart 60km/t brukes 60 min, altså er kjørt strekning 60 km. Vi har at

$v = \frac{s}{t}$

Vi ser for eksempel at om man kjører med 40km/t så tar det 90 min som er 1,5 time. Så fart og tid er omvendt proporsjonale.

b)

Siden begge øker kan vi utelukke omvendt proporsjonalitet. Siden den ene firdobles når den andre dobles er de ikke proporsjonale. De er ingen av delene.

c)

Oppgave 4

a)

Det ser jo ganske riktig ut......

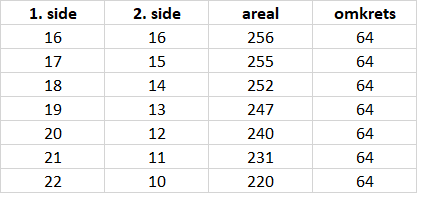
b)

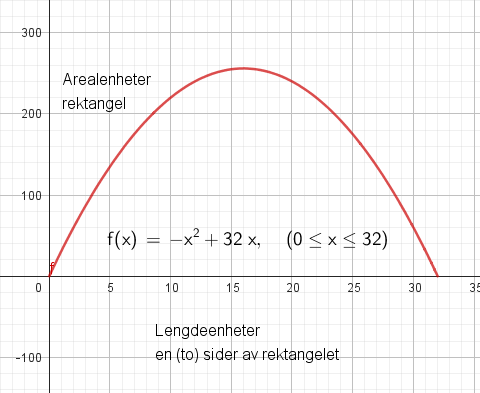
I et rektangel er to og to sider like lange (rettvinklet). Dersom vi har 64 meter til rådighet har to av sidene lengden x. Det som er igjen av lengde er da 64 - 2x fordelt på de to andre sidene, En av disse sidene blir da 32-x (har delt på to).

En funksjon for arealet blir da $A(x) = x \cdot (32-x)= -x^2 + 32x$

Vi observerer at man får det største arealet ved å lage et kvadrat (sidelengde 16 m), som er et spesialtilfelle av et rektangel.

Oppgave 5

a)

Lars ønsker å finne nullpunktet til funksjonen. Resultatet blir at programmet skriver ut tallet 5 (som er x-verdien i nullpunktet til funksjonen).

b)

Resultatet vil bli at programmet skriver ut 2 og 4, som er x-verdiene til nullpunktene til denne funksjonen.

c)

Nullpunktene til denne funksjonen er x=-12 og x=12. I linje 4 må Lars definere x=-12 (eller lavere), og i linje 6, må Lars la while-løkken gå til x<=12 (eller høyere).

Oppgave 6

a)

Bruker regresjonsanalyse i Geogebra. Modellen blir $S(x)=2.03x^{0.47}$

b)

$\sqrt{9.81}\approx 3,13$ og $\pi\approx 3,14$, så vi kan forkorte pi med roten av g i formelen. Dermed har vi:

$T=2\pi\sqrt{\frac{L}{g}} = 2\pi\frac{\sqrt{L}}{\sqrt{g}}\approx 2\sqrt{L}$

c)

Vi kaller snorlengden for x og svingetiden for S(x). Da er formelen fra oppgave b) slik: $S(x)=2\sqrt{x}$

Dette er tilnærmet samme formel som i oppgave a). $\sqrt{x}$ er det samme som $x^{0.5}$, så vi kan skrive formelen fra c) som $S(x)=2x^{0.5}$. Vi ser at dette er veldig likt formelen i oppgave a).

Oppgave 7

Cooper-testen:

$\frac{380\,m}{3\,min}\cdot 12\,min=380\,m\cdot 4=1520\,m$.

På 12 min kan Sofie løpe 1,52 km.

Kilokalorier:

$\frac{32\,kcal}{3\,min}\cdot 60\,min = 32\,kcal\cdot 20 = 640\,kcal$

Dersom Sofie løpet i 60 minutter, forbrenner hun 640 kcal.