DEL 1

Oppgave 1

Renten på et lån steg fra 2,0 % til 2,2 %.

a)

Renten steg med 0,2 prosentpoeng. Utregning: 2,2 - 2,0 = 0,2

b)

Deler endringen i prosentpoeng på opprinnelig rente:

$\frac{0,2}{2,0}=\frac{2}{20}=\frac{10}{100}=10$ %.

Renten steg med 10 prosent.

Oppgave 2

Leser av diagrammet og finner antall elever de ulike årene:

2018: 700 elever

2019: 800 elever

2020: 900 elever

2021: 1000 elever

Antall elever øker med 100 hvert år. Det var størst prosentvis økning i antall elever fra 2018 til 2019, fordi 100 er en større andel av 700, enn det er av 800, 900 eller 1000.

Oppgave 3

a)

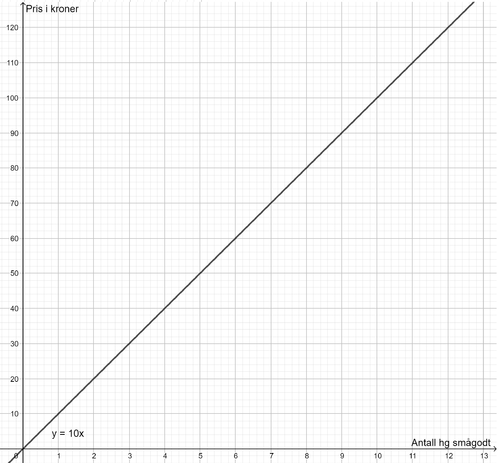
To størrelser som er proporsjonale er for eksempel antall hektogram smågodt kjøpt i butikken, og prisen man betaler. For eksempel koster det 10 kr for 1 hg, 20 kr for 2 hg og så videre. Prisen øker altså jevnt (med samme stigningstall). Kjøper man ingenting, koster det heller ingenting (det er ikke noe konstantledd).

b)

Siden dette er del 1, må du tegne grafen til din funksjon for hånd.

Oppgave 4

a)

$V(x) = 4x^3 −100x^2 +600x \quad, \quad 0<x<10$

$V(5)= 4\cdot5^3 -100\cdot 5^2 +600\cdot 5 = 4\cdot 125 - 100\cdot 25 + 3000 = 500 - 2500 + 3000 = 1000$

Dersom Siri lager esken 5 cm høy, får den et volum på 1000 kubikkcentimeter.

b)

Dersom Siri løser likningen $V(x)=500$, finner hun ut hvor høy esken må være (x), for at den skal ha et volum på 500 kubikkcentimeter.

Oppgave 5

Eleven ønsker å finne ut hvor mange år det tar før en verdi på 2000 (for eksempel kroner) har økt til 4000 (eller mer), med en årlig økning på 5%.

I linje 1-4 defineres variablene startverdi, verdi, vekstfaktor og år. Variabelen "verdi" settes til samme verdi som "startverdi", altså 2000. I linje 6-8 har vi en while-løkke som gjentar seg så lenge "verdi" er mindre enn det dobbelte av "startverdi", altså 4000. Inni løkken ganger "verdi" med "vekstfaktor" for å få en 5% økning på "verdi", og variabelen "år" økes med én. Etter at løkkes avsluttes, skrives "verdi" og "år" ut på skjermen (linje 10 og 11). "verdi" vil være 4000 eller mer, og "år" forteller oss hvor mange år dette har tatt.

Oppgave 6

$A=l\cdot b = 3b\cdot b = 3b^2$

Setter arealet til 432 kvadratcentimeter:

$3b^2=432$

$b^2 =\frac{432}{3}$

$b^2 =144$

$b=\sqrt{144}$

$b=12$

Rektangelet er 12 cm bredt.

DEL 2

Oppgave 1

Løser oppgaven i Geogebra.

a)

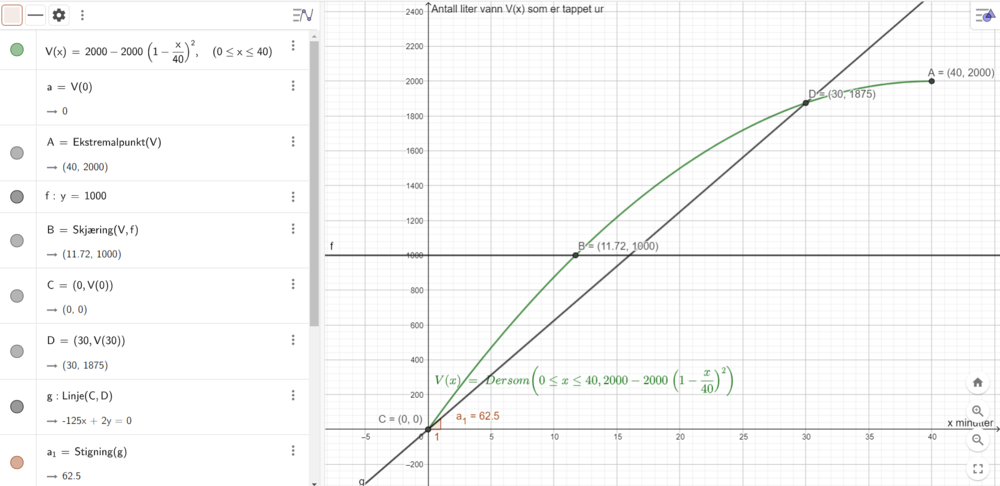
$V(0)=0$ (se algebrafeltet på skjermbildet). Det vil si at før tappingen starter (ved 0 minutter), så har det ikke blitt tappet ut noe vann av tanken (0 liter).

b)

Verdimengden til V er 2000. Jeg fant høyeste punkt på grafen, A=(40,2000), ved å bruke knappen "Ekstremalpunkt". Laveste punkt er (0,0). Verdimengden er da 2000 - 0 = 2000.

c)

Lager linjen y = 1000, og bruker knappen "skjæring mellom to objekt" mellom linjen og grafen til V. Får punkt B=(11.7, 1000). Det vil si at det tar 11,7 minutter før halvparten av vannet er tappet ut av tanken. Se punkt B.

d)

Lager punkt C=(0,V(0)) og D=(30,V(30)), og lager en linje som gå gjennom disse to punktene med knappen "linje". Finner stigningstallet til linjen med knappen "stigning". Stigningstallet er 62,5 (se verdien a1 i algebrafeltet). Svaret forteller oss at fra 0 til 30 minutter etter at tappingen har startet, tappes vannet med en gjennomsnittlig fart på 62,5 liter per minutt.

e)

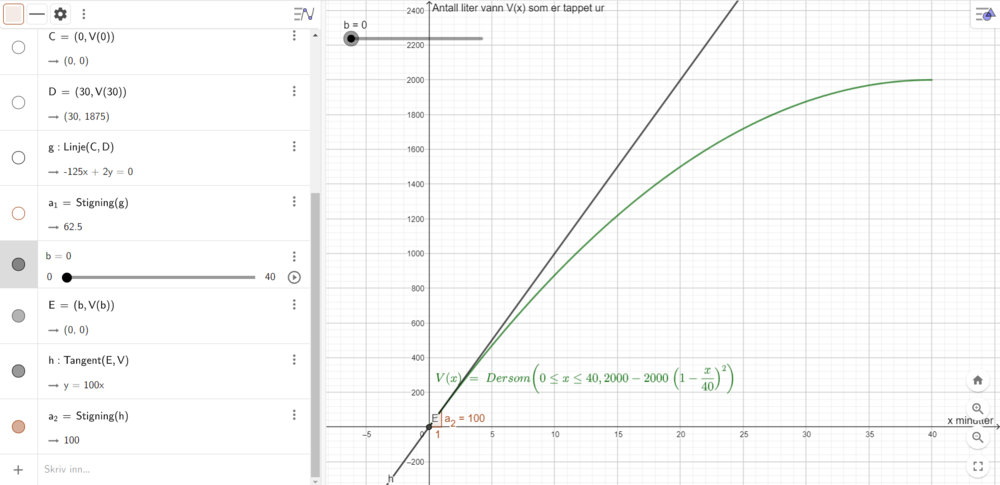
Lager en glider b med kommandoen "glider(0,40,1)". Lager et punkt E=(b,V(b)) og tangenten til V i punktet E med knappen "tangenter". Viser stigningstallet til tangenten med knappen "stigning". Flytter på glideren slik at punkt E flytter seg langs hele grafen til V, og ser om stigningstallet noen gang overstiger 105. Jeg finner at det høyeste stigningstallet er 100, når E=(0,0). Se verdien a2 i algebrafeltet.

Det vil altså aldri tappes mer enn 105 liter i løpet av ett minutt.

Oppgave 2

a)

Grafen starter i 600 på y aksen, altså er konstantleddet b= 600. Vi ser at grafen øker med 100 når x verdien øker med 25, altså er stigningstallet 4 : A(x) = 4x + 600.

b)

Vi leser av grafen. 50 km på x aksen gir 1000 kroner på firma B. Det kaster altså 1000 kroner å kjøre 50 km. Det blir 20 kr per km.

Vi legger merke til at i firma B øker prisen med 100 kr per 50 km. 400 km koster da 1600 kroner, som blir 4 kr per kilometer.

I begge tilfeller deler man kostnad på antall kilometer.

c)

Det er 97 km. Firma A og C er like dyre dersom man kjører 100 km, så han bør velge ett av disse. Kjører man over 200 km er firma B billigst.

Oppgave 3

Vi gjør om til prosent avslag per flaske:

A: $1- \frac{2}{3} = 0,33 = 33 $ % rabatt.

B: 30% rabatt

C: $1 - \frac{1,25}{2} = 0,375 = 37,5$ % rabatt.

1P 2022 vår LK20 LØSNING

DEL 1

Oppgave 1

a)

b)

Oppgave 2

Oppgave 3

a)

b)

Oppgave 4

a)

b)

Oppgave 5

Oppgave 6

DEL 2

Oppgave 1

a)

b)

c)

d)

e)

Oppgave 2

a)

b)

c)

Oppgave 3

Oppgave 4

a)

b)

Oppgave 5

Oppgave 6

a)

b)

c)

Oppgave 7

a)

b)

c)

d)

e)

Oppgave 8

a)

b)

c)

d)