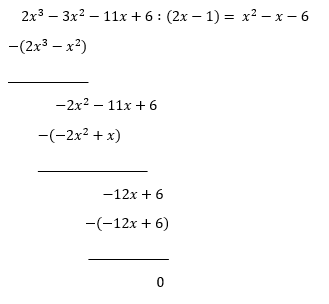DEL 1

Oppgave 1

a)

$f(x)=x^3+2x^2-\sqrt{x} \\ f'(x)=3x^2+4x-\frac{1}{2\sqrt{x}}$

b)

$g(x)=x^2\cdot ln(2x-1) \\ g'(x)=2x\cdot ln(2x-1)+\frac{2x^2}{2x-1}$

Brukte produktregelen og kjerneregelen. Løsningen kan evt. faktoriseres.

c)

$ h(x) = \frac{4x}{e^{2x}} \\ h'(x)=\frac{4e^{2x}-4x\cdot 2e^{2x}}{(e^{2x})^2} \\ = \frac{e^{2x}(4-8x)}{(e^{2x})(e^{2x})} = \frac{-8x+4}{e^{2x}}$

Oppgave 2

a)

$\frac{1}{x^2-x}+\frac{1}{x^2+x}-\frac{1}{x^2-1} \\ = \frac{1}{x(x-1)}+\frac{1}{x(x+1)}-\frac{1}{(x+1)(x-1)} \\ = \frac{x+1}{x(x-1)(x+1)}+\frac{x-1}{x(x+1)(x-1)}-\frac{x}{x(x+1)(x-1)}\\ = \frac{x+1+x-1-x}{x(x+1)(x-1)} \\ = \frac{x}{x(x+1)(x-1)} \\ = \frac{1}{x^2-1}$

b)

$\frac{(ln\,e^3+1)^2}{(e^{ln\,3}+1)} = \frac{(3+1)^2}{(3+1)^3}=\frac{4^2}{4^3}=\frac{1}{4}$

Oppgave 3

a)

$(2x-1)=0 \\ x=\frac{1}{2}$

Sjekker om $x=\frac{1}{2}$ er et nullpunkt for $f(x)$:

$f(\frac{1}{2})= 2(\frac{1}{2})^3-3(\frac{1}{2})^2-11\cdot \frac{1}{2}+6 \\ = \frac{2}{8}-\frac{3}{4}-\frac{11}{2}+6 \\ = \frac{2}{8}-\frac{6}{8}-\frac{44}{8}+6 \\ = \frac{-48}{8}+6 = -6+6 = 0$

$x=\frac{1}{2}$ er et nullpunkt for $f(x)$, det vil si at divisjonen $f(x):(2x-1)$ går opp.

b)

Utfører polynomdivisjonen $f(x) : (2x-1)$

$x^2-x-6=(x-3)(x+2)$

$f(x)=(2x-1)(x-3)(x+2)$

c)

$f(x) \geq (2x-1)(x+2) \\ (x-3)(2x-1)(x+2) \geq (2x-1)(x+2) \\ (x-3)(2x-1)(x+2) - (2x-1)(x+2) \geq 0$

Setter felles faktor $(2x-1)(x+2)$ utenfor parentes.

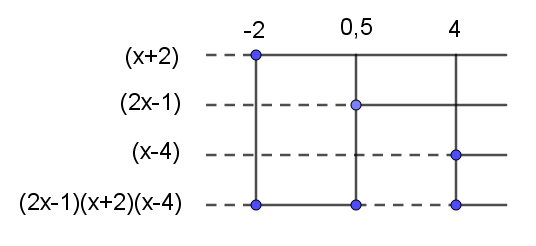
$ (2x-1)(x+2)((x-3)-1) \geq 0 \\ (2x-1)(x+2)(x-4) \geq 0 $

$f(x) \geq (2x-1)(x+2)$ når $x \in [-2, \frac{1}{2}] \cup [4,\rightarrow \rangle$

Oppgave 4

a)

Vi har punktene $A(1,3)$ og $B(5,-1)$

$\vec{AB}=[5-1,-1-3]=[4,-4]$

$|\vec{AB}|=\sqrt{4^2+(-4)^2}=\sqrt{32}=\sqrt{2\cdot 16}=4\sqrt{2}$

b)

Likning for en sirkel med sentrum i $(x_0, y_0)$:

$ (x - x_0)^2 + (y - y_0)^2 = r^2 $

Husk at sirkelens diameter er fra punkt A til punkt B. Sentrum i vår sirkel blir midt mellom punkt A og B, i (3,1).

Radius blir halvparten av $|\vec{AB}|$: $\frac{4\sqrt{2}}{2}= 2\sqrt{2}$

Vi setter inn våre verdier og får likningen for sirkelen:

$ (x - 3)^2 + (y - 1)^2 = (2\sqrt{2})^2 \\ (x-3)^2 + (y-1)^2 = 4\cdot 2 \\ (x-3)^2 + (y-1)^2 = 8 $

c)

For å få en rett vinkel i C, må punkt C ligge på sirkelperiferien. Dette på grunn av Thales setning.

Sentrum av sirkelen er i punkt (3,2), og radiusen av sirkelen er $2\sqrt{2}$. Siden $3+2\sqrt{2} < 6 $, så tangerer ikke linja x=6 sirkelen. Dermed er punkt C utenfor sirkelperiferien, og det er ikke mulig å plassere C slik at trekanten ABC får en rett vinkel i C.

En annen måte å finne ut av det er å sjekke om det finnes en y-verdi for punkt C hvor $\vec{AC}\cdot \vec{BC} = 0$.

Oppgave 5

a)

$\binom{10}{3} = \frac{10 \cdot 9 \cdot 8}{3 \cdot 2 \cdot 1} = 10 \cdot 3 \cdot 4 = 120 $

120 ulike grupper på tre deltakere kan komme til finalen.

b)

Vi har flere kvinner enn menn en gruppe på tre, dersom vi har to eller tre kvinner.

P(to eller tre kvinner) = $\frac{\binom{5}{2} \binom{5}{1}}{ \binom{10}{3}} + \frac{\binom{5}{3} \binom{5}{0}}{ \binom{10}{3}} = \frac{10 \cdot 5}{120} + \frac{10 \cdot 1 }{120} \\ = \frac{60}{120} = \frac{1}{2}$

60 av de 120 gruppene, det vil si halvparten, inneholder flere kvinner enn menn.

R1 2019 vår LØSNING

Innhold