2P 2017 vår LØSNING

Løsning bidratt av Lektor Ørjan Augedal, Fana privat gymnas

Diskusjon av denne oppgaven

Oppgave 1

0,0,0,0,0,1,1,1,1,1,1,2,2,3,3,4

Variasjonsbredde: 4 -0 =4 ( største minus minste)

Typetall: 1 (den det er mest av)

Median 1 ( den i midten når materialet er organisert stigende)

Gjennomsnitt; Sum søsken delt påantall elever: $\frac {20}{16}= \frac{5}{4} = 1,25$

Oppgave 2

$\frac{25}{125} = \frac{1}{5}= 20%$

20% tok bussen den dagen.

Oppgave 3

$5^0 \cdot 2^3 \cdot 8^{-2}\cdot (4^{-1})^{-3} \\ = 1 \cdot 8 \cdot \frac{1}{64} \cdot 4^3 \\ =8 $

Oppgave 4

I 10 liter vann, som er det samme som 100 dL vann er det ca. $3,0 \cdot 10^{25}$

For å finne antall molekyler i 1,5 dL, deler vi på 100 og ganger med 1,5:

$3,0 \cdot 10^{25} \cdot \frac{1,5}{100} = 4,5 \cdot 10^{23}$

Oppgave 5

a)

Dersom noe vokser periodisk med en fast størrelse har man en lineær sammenheng:

$f(x)= 80000x + 1200000$

b)

Dersom noe vokser periodisk med en fast prosent er veksten eksponentiell. Vekstfaktoren her er 1,08:

$g(x)= 1200000 \cdot 1,08^x$

c)

B er rettlinjet og KAN beskrive f.

A later til å være eksponentiell og KAN beskrive g.

Både A og C vokser, men ved eksponentiell positiv vekst vil den momentane veksten øke med tiden. Det er tillfelle i A. I graf C avtar den.

Oppgave 7

b)

Vi setter figurnummer lik n.

Figur en har en mere enn det dobbelte av figurnummeret: 1 pluss 2 ganger 1.

Figur 2: 1pluss 2 ganger 2.

Figur 5: 1 pluss 2 ganger 5.

Figur n: 2n+1.

c)

Omkretsen er hele tiden to mere enn figurnummeret. Altså n+2.

d)

Finner antall pinner i omkretsen ved å dele på 2,5.

104 : 2,5 =42 pinner

Fra oppgave c ser man at det er snakk om figur nr. 40. Fra oppgave b finner man antall pinner totalt til å være 2n+1 = 81 pinner.

Oppgave 1

a)

b)

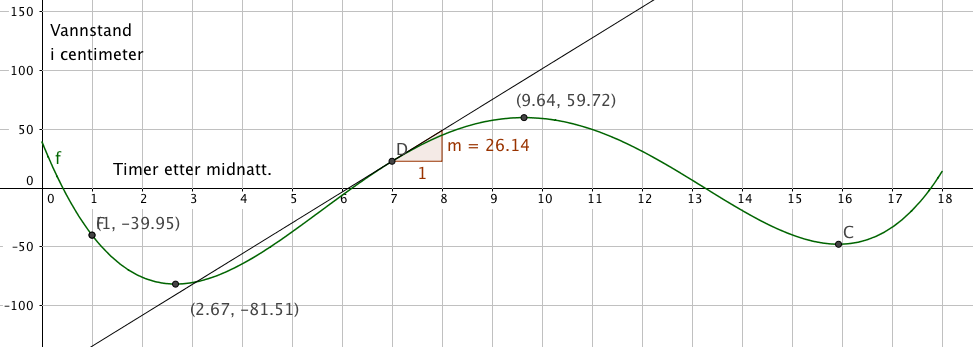
Vi ser ar f(1) er ca. - 40 cm (markert) og at f(12) er ca. 31 cm (ikke markert), fra fuguren i a.

c)

Fra Figuren i a ser man at den største forskjellen er 59,72+ 81,51 = 141,23 cm. Altså ca. 141 cm i fieskjell.

d)

Den momentane veksten er 26,14cm/time kl 07. 00. Det betyr at vannet stiger med en hastighet på 26 cm/time kl 07:00.

Oppgave 2

$x \cdot 1,15 = 3703000 \\ x = \frac{3703000}{1,15} = 3220000$

Prisantydning var på 3 220 000 kr.

Oppgave 3

$x \cdot 1,0425^{20} = 1724180 \\ x = \frac{1724180 }{1,0425^{20}} = 750000$

Hun arvet 750 tusen kroner.

Oppgave 4

Et legeme beveger seg med konstant hastighet bort fra utgangspunktet. Etter en stund beveger det seg tilbake til utgangspunktet med en konstant hastighet som er ca. dobbelt så stor som hastigheten bort fra utgangspunktet.

Oppgave 5

a)

Vi vet at søylehøyde er frekvens delt på klassebredde. Søylehøyden leser vi av i figuren. Vi har tre søyler og får:

$$