Praktiske problemer der differensiallikninger er løsningen
UNDER KONSTRUKSJON
Svingninger
Frie svingninger uten dempning
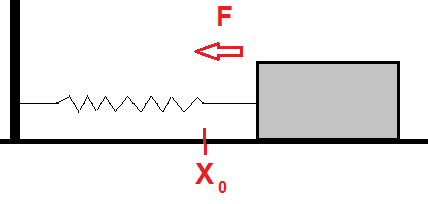
En kloss ligger på et friksjonsfritt underlag. Klossen er festet til en fjær som er fastspent i veggen slik figuren viser. Likevektspunktet er
Newtons andre lov sier at summen av kreftene som virker på klossen er lik masse multiplisert med akslerasjon.
Hooks lov sier at:
F = -kx
k er fjærkonstanten. Kraften er proporsjonal med utslaget og virker hele tiden mot likevektspunktet.
Vi får:
som er identisk med
Her finner du hvordan disse likningene løses:
[[1]]
Eksempel 1:
En kloss med masse 0,75 kg. ligger på en friksjonsfri overflate og er festet til en forankret fjær. Fjæren strekkes 1,5 meter med en kraft på 200 Newton.
Klossen trekkes ut 0,6 meter mot høyre, fra likevektspunktet, der den slippes. Beskriv bevegelsen.
Frie svingninger med dempning
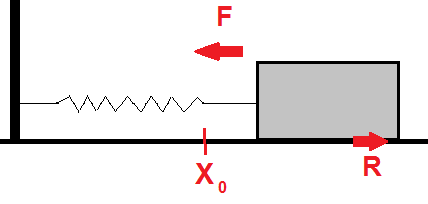
En kloss ligger på et underlag med friksjon. Klossen er festet til en fjær som er fastspent i veggen slik figuren viser. Likevektspunktet er
Man antar at friksjonen R er proporsjonal med farten v og virker mot bevegelsen. v er x' og R = rx'
mx + rx' + kx = 0 eller
<math> x^{}+ \frac rm x^' + \frac km =0 </math>
Naturlig vekst
Dersom en størrelse x vokser med tiden, kan det skrives som
der k er en konstant og x = x(t).
Man får
A er konstanten eC og man observerer at vet tiden t = 0 er A = x, dvs. A =x0
Altså:
Dersom k > 0 har man en vekstsituasjon.
Dersom k < 0 har man en situasjon der en størrelse avtar, foreksempel aktiviteten i et radioaktivt materiale:
k er isotipavhengig ( dersom modellen representerer aktivitet i radioaktivt materiale).
Dersom man har en populasjon kan modellen over være egnet til å beskrive veksten i startfasen, men ingen populasjoner vokser i det uendelige. En mer egnet modell kan da være den logistiske.
Logistisk vekst
Man tenker at populasjonsveksten vil stagnere når antall individer nærmer seg det et område kan tåle. Det antall kalles bæreevnen og vil variere ut fra økosystemets forutsetninger. Man kaller bæreevnen for B
Den relative vekstraten er
Ved tiden t = 0 er
Da er
som gir
Ved noe regning får man
Newtons avkjølingslov ( og oppvarming)
Hvordan går det egentlig med et legeme med romtemperatur, når den slippes i kokende vann?
Den momentane temperaturendringen er
T(t) - er objektets temperatur ved tiden t.
Tomg - er omgivelsenes temperatur.
T(0) - er objektets temperatur ved tiden t = 0, dvs. i det øyeblikket det befinner s.
Newtons avkjølingslov sier at temperaturendringen
er proporsjonal med differansen mellom T(t) og Tomg, dvs:
k er en konstant som blant annet har med legemets varmeledningsevne og geometri å gjøre.
Her har man to muligheter:
Avkjøling
Dersom objektet er varmere enn omgivelsene ved tiden t = 0 har man en avkjølingssituasjon. Da er
negativ. Det gir: <math> (T(t) - T_{omg}) > 0</math>
Oppvarming
Dersom objektet er kaldere enn omgivelsene ved tiden t = 0 har man en oppvarmingssituasjon. Da er
positiv. Det gir:
Det gir Newtons lov for avkjøling:
Eks 8:
En smed skal bearbeide et stykke metall. Når det tas ut av ovnen er det 500°C. Metallet lar seg bearbeide til det er 150°C. Under denne temperatur er det vanskelig å forme. Smeden har fra tidligere erfaringer funnet ut at metallet avkjøles med 200 grader de første 10 minuttene. I rommet der arbeidet foregår er det 30°C.
Hvor lang tid har smeden på bearbeidingsprosessen?
Løsning:
Newtons lov for avkjøling sier:
I dette tilfellet gir det:
<math>\frac{dT}{dt} = -k(T(t) - 30) \ \frac{dT}{dt} = k(23 - T(t))\ \int \frac {1}{23 - T(t)})dT = \int(k)dt \ - ln (23 - T(t)) = kt + C \
23 - T(t) = e^{-(kt + C)} </math>
<math>23 - T(t) = C_2e^{-kt } \ \hspace{50 mm} der \hspace{5 mm}C_2 \hspace{5 mm}er\hspace{5 mm} e^C \
T(t) = 23 - C_2e^{-kt } \hspace{50 mm} </math>
Man har oppgitt:
Hva er k?
k er en konstant som bestemmes av objektets form og materialegenskaper,
samt omgivelsenes tetthet / varmelednigsegenskaper mm.
For å finne k må man benytte seg av smedens erfaringer og kunnskaper:
Det gir funksjonen for avkjøling:
<math>
T(t) = 470 e^{-0,0449t}</math>
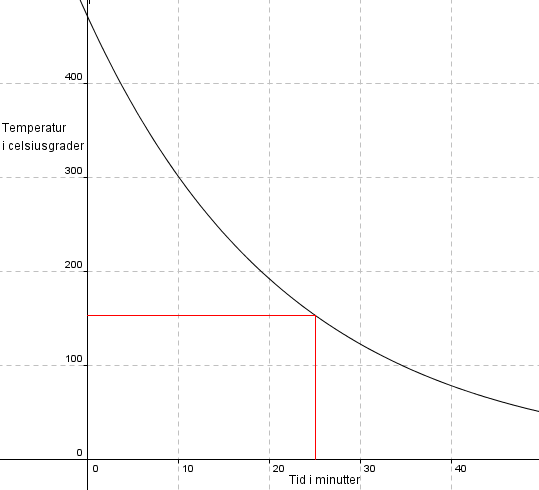
Hvor lang tid har så smeden før arbeidsstykket hans går under 150?
t = 25 min
Temperaturforløpet ser slik ut: