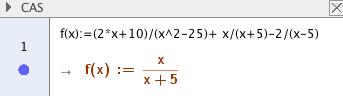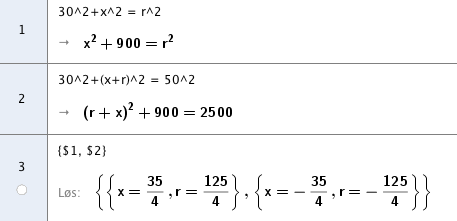R1 eksempeloppgave 2015 vår LØSNING
- Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du oppdager feil i fasit. På forhånd, takk.
DEL EN
Oppgave 1
a)
$f(t)=0.02t^3+0.6t^2+4.1\\f'(t)=0.06t^2+1.2t$
b)
$g(x)=x^2\cdot \ e^{2x}\\g'(x)=2x\cdot \ e^{2x}+x^2\cdot \ 2e^{2x}=2x\cdot \ e^{2x} (1+x)$
c)
$h(x)=ln(x^3+1)\\h'(x)=(ln u)'\cdot \ (x^3+1)' \ = \frac{1}{x^3+1}\cdot \ 3x^2 \ =\frac{3x^2}{x^3+1}$
Opgave 2
a)
$f(x)=x^3+ax^2-13x+15$. Hvis $f(x)$ er delelig med $(x-1)$, er $f(1)=0 \\ $ $1^3+a\cdot \ 1^2-13 \cdot \ 1 +15=0 \\ 1+a+2=0 \\ a=-3$
b)
$ \quad(x^3-3x^2-13x+15):(x-1)=x^2-2x-15\\-(x^3-x^2) \\ \quad \quad -2x^2-13x \\ \quad \quad -(-2x^2+2x) \\ \quad \quad \quad \quad -15x+15 $
Faktoriserer $x^2-2x-15$ ved abc-formelen. Da får vi at $x=5 \vee x=-3$
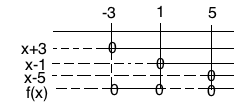
$f(x)$ kan da skrives som $(x+3)(x-1)(x-5)$ , hvor alle ledd er av første grad.
Må så tegne et fortegnsskjema åg finne ut når f(x) er mindre eller lik null:
$x \in < \leftarrow, -3] \cup [1,5]$
Oppgave 3
Vi har en hypergeometrisk situasjon:
$\frac{\binom{7}{2} \binom{5}{1}}{\binom{12}{3}} = \\ \frac {7 \cdot 3 \cdot 5}{4 \cdot 11 \cdot 5} = \\ \frac {21}{44}$
Det er 21/44 sannsynlig at det blir to jenter og en gutt i gruppa.
Oppgave 4
$\frac{x+2}{x^2-16} + \frac {x}{x+4} - \frac{2}{x-4} =\\ \frac{x+2+x(x-4)-2(x+4)}{ ((x+4)(x-4)} =\\ \frac{x+2+x^2-4x-2x-8}{(x+4)(x-4)} = \\ \frac{x^2-5x-6}{(x+4)(x-4)} = \\ \frac{(x+1) (x-6)}{(x+4)(x-4)}$
Oppgave 5
a)
$\frac{a^2(b^2)^2}{a^{-3}b^0} = \\ \frac{a^2b^4}{a^{-3}}= \\ a^{2+3}b^4 = \\ a^5b^4$
b)
$lg(a^2 b)+ lg(ab^2)+lg (\frac{a}{b^3}) = \\ 2lg a +lg b + lg a + 2 lgb +lg a - 3lg b = \\ 4 lg a$
Oppgave 6
$2^3+2^3+2^3+2^3 = 2^n \\ 4 \cdot 2^3 = 2^n \\ 2^2 \cdot 2^3 = 2^n \\ 2^5 = 2^n \\ n=5$
Oppgave 7
$x^2+5x+6=0 \\ (x+2)(x+3)= 0$
Likningen har løsninger for x=-2 eller for x=-3. Implikasjonspilen må derfor gå fra høyre mot venstre. Altså, x= -2 impliserer løsning. Siden -3 også er en løsning kan ikke implikasjonen gå andre veien, og vi har ikke ekvivalens.
Oppgave 8
a)
$\vec{AB} = [3-1, 4-0] = [2,4] \\ \vec{AC} =[2-1, t-0]= [1,t]$
b)
$\vec{AB} \cdot \vec{AC} =0 \\ [2,4] \cdot [1,t] = 0 \\ 2+4t =0 \\ t = - \frac 12$
c)
$[2,4] =k [1,t] \\ k=2 \wedge 4 = kt$
Det gir t = 2.
Oppgave 9
a)
Nullpunkt:
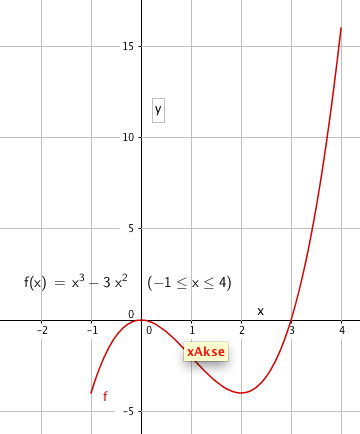
$f(x)=0 \\ x^2(x-3) =0 $
Nullpunkt (0, 0) og (3, 0)
Ekstremalpunkt:
$f´(x)= 0 \\3x^2 - 6x=0 \\3x(x-2)=0$
Det ser ut som om funksjonen kan ha ekstremalpunkter for x=0 og x=2, men vi må sjekke fortegnet for den deriverte på begge sider av x. Om vi ikke får fortegnsskifte er det et terassepunkt, og ikke et ekstremalpunkt.
f´(-1) = 9 og f´(1) = -3, det betyr at x = 0 gir et maksimumspunkt. f´(4) = 24, igjen har vi fortegnsskifte. Det betyr at funksjonen har et minimumspunkt for x = 2.
Maksimum: (0,0)
Minimum: (2, -4)
b)
c)
Vi dobbelderiverer for å finne vendepunkt:
$f´´(x)= 6x-6 \\ f´´(x) =0 \\ x=1$
f(1) = - 2
Funksjonen har et vendepunkt i (1,-2). Tangenten i dette punktet er parallell med funksjonen akkurat i punktet. Selv om den skjærer gjennom grafen til gunksjonen kalles den for en vendetangent. f´(1) = -3, det betyr at stigningstallet til tangenten er -3. Likningen for denne er:
$y= ax + b \\ -2 = -3 \cdot 1+ b \\ b= 1 \\ y = -3x + 1$
Oppgave 10
a)
Trekanten ABE er ideintisk med trekanten ECD. Begge har en vinkel på 90 grader. Summen av de to andre er 90 grader. Det betyr at vinkel BEA og vinkel CED tilsammen er 90 grader. Derfor er vinkel AED 90 grader.
b)
Arealer trekanter:
$\triangle ABE = \frac{ab}{2} \\ \triangle DCE = \frac{ab}{2} \\ \triangle AED = \frac{c^2}{2}$
Arealet av trapeset er:
$A_t = \frac{a+b}{2} (a+b)$
c)
Vi setter arealet av trapeset lik arealet av de tre trekantene og får:
$\frac{a+b}{2} (a+b)= \frac {ab}{2} + \frac{ab}{2} + \frac{c^2}{2} \\ (a+b)(a+b)= c^2 + 2ab \\ a^2 + 2ab + b^2 = c^2 + 2ab \\ a^2 + b^2 = c^2$
(Lurer på om dagens presidentkandidater fikser det like bra :-))
Oppgave 11
$x^2+y^2-4x+6y-12 =0 \\ (x^2-4x+4)+(y^2+6y+9) -12-13 =0 \\(x-2)^2 + (y+3)^2 = 5^2$
Sirkelen har radius 5, med sentrum i (2, -3).
Oppgave 12
a)
CEF er en likebeint trekant. Derfor er EC = CF = $\beta$
BDE er også en likebeint trekant, derfor er BD = $\alpha$
b)
c)
DEL TO
Oppgave 1
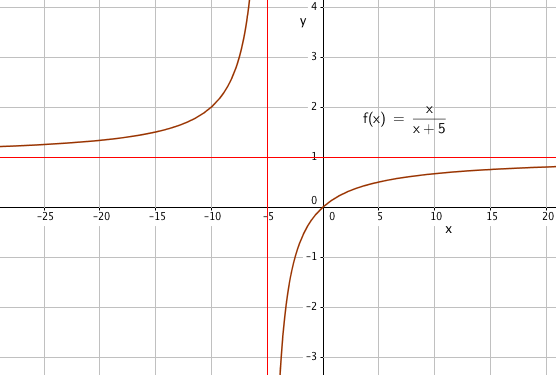
Den opprinnelige funksjonen er ikke definert for x= 5.
Funksjonen er kontinuerlig og deriverbar for $x \in \R \backslash \{ -5, 5 \} $.
Oppgave 2
Radius er 31,25