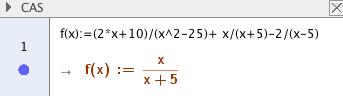R1 eksempeloppgave 2015 vår LØSNING

• Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du oppdager feil i fasit. På forhånd, takk.

DEL EN

Oppgave 1

a)

$f(t)=0.02t^3+0.6t^2+4.1\\f'(t)=0.06t^2+1.2t$

b)

$g(x)=x^2\cdot \ e^{2x}\\g'(x)=2x\cdot \ e^{2x}+x^2\cdot \ 2e^{2x}=2x\cdot \ e^{2x} (1+x)$

c)

$h(x)=ln(x^3+1)\\h'(x)=(ln u)'\cdot \ (x^3+1)' \ = \frac{1}{x^3+1}\cdot \ 3x^2 \ =\frac{3x^2}{x^3+1}$

Opgave 2

a)

$f(x)=x^3+ax^2-13x+15$. Hvis $f(x)$ er delelig med $(x-1)$, er $f(1)=0 \\ $ $1^3+a\cdot \ 1^2-13 \cdot \ 1 +15=0 \\ 1+a+2=0 \\ a=-3$

b)

$ \quad(x^3-3x^2-13x+15):(x-1)=x^2-2x-15\\-(x^3-x^2) \\ \quad \quad -2x^2-13x \\ \quad \quad -(-2x^2+2x) \\ \quad \quad \quad \quad -15x+15 $

Faktoriserer $x^2-2x-15$ ved abc-formelen. Da får vi at $x=5 \vee x=-3$

$f(x)$ kan da skrives som $(x+3)(x-1)(x-5)$ , hvor alle ledd er av første grad.

Oppgave 9

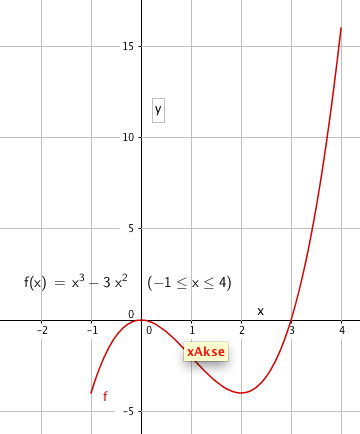
a)

Nullpunkt:

$f(x)=0 \\ x^2(x-3) =0 $

Nullpunkt (0, 0) og (3, 0)

Ekstremalpunkt:

$f´(x)= 0 \\3x^2 - 6x=0 \\3x(x-3)=0$

Det ser ut som om funksjonen kan ha ekstremalpunkter for x=0 og x=3, men vi må sjekke fortegnet for den deriverte på begge sider av x. Om vi ikke får fortegnsskifte er det et terassepunkt, og ikke et ekstremalpunkt.

b)

Oppgave 10

a)

Trekanten ABE er ideintisk med trekanten ECD. Begge har en vinkel på 90 grader. Summen av de to andre er 90 grader. Det betyr at vinkel BEA og vinkel CED tilsammen er 90 grader. DErfor er vinkel AED 90 grader.

Oppgave 11

$x^2+y^2-4x+6y-12 =0 \\ (x^2-4x+4)+(y^2+6y+9) -12-13 =0 \\(x-2)^2 + (y+3)^2 = 5^2$

Sirkelen har radius 5, med sentrum i (2, -3).

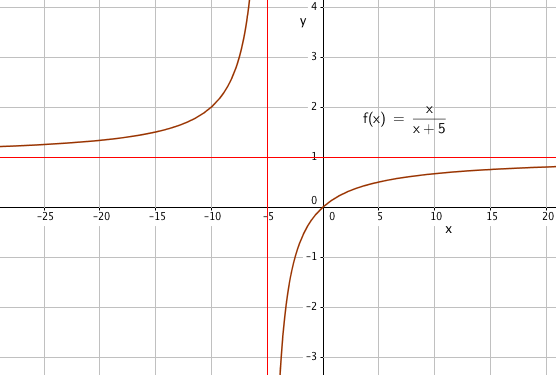
Oppgave 1

Funksjonen er kontinuerlig og deriverbar for $x \in \R \ { -5 } $.