2P 2015 høst LØSNING
DEL EN
Oppgave 1
70% er det samme som 280 kroner. 280: 70 = 4. Dvs 1% er 4 kroner. Da er 100% lik 400 kroner. (Finnes flere andre, mer elegante måter å gjøre det på også).
Oppgave 2
Oppgave 3
Oppgave 4
Beløpet hun vant: x
Vekstfaktor til 3,2%: 1,032
Tid: 10 år
Uttrykk :
Oppgave 5
Omkrets av jorden: 40 000km = 40 000 000 meter.
Antall personer:
Altså ca. 25 millioner mennesker (mange av dem må være svømmedyktige).
Oppgave 6
a)
Når man jobber med klassedelt materiale må man forutsette at observasjonene fordeler seg jevnt utover i klassens intervall. Dette er trolig ikke tilfelle, men det beste vi kan forutsette siden vi ikke har detaljkunnskap inne hver klasse. Feilen fra denne forutsettningen blir ofte liten. Median av hundre verdier er gjennomsnittet av verdi 50 og 51. Vi ser at i bedrift A er begge disse i klassen 20 - 40 år. Dvs medianalderen er under 40 år i bedrift A. I bedrift B ligger den i klassen 40 - 60 år, altså høyerer.
b)
Gjennomsnittet i klassedelt materiale finnes ved å finne klassemidtpunktene i hver av klassene og gande disse med respektive frekvenser. Summer alt og del på antall observasjoner.
Gjenneomsnitt bedrift B:
Gjennomsnittsalderen er ca 46 år i bedrift B.
Oppgave 7
a)
Vi har to punkter og skal lage en lineær modell, (1,60) og (5,90). På 4 uker øker treningsmengden med 30 minutter.
På en uke øker den med
y= ax + b.
I vårt tillfälle blir det
y= 7,5x + b
Vi bruker første punktet (1, 60) og setter inn for x og y og får
Modellen blir da
y = 7,5x + 52,5
b)
I uke 40 betyr det at x = 40 i uttrykket:
Hun må trene 5 timer og 52 minutter og 30 sekunder, eller ca. seks timer i uken.
Oppgave 8
Vi leser av figuren i oppgaven og ser at startverdien er 10 000 bakterier. Etter en time er det 9000 bakterier. Det betyr at antall bakterier minker med 10% per time. Det gir en vekstfaktor på 0,90.
Uttrykket blir da:
Der x er tidsenheter, i dette tilfelle timer.
Oppgave 9
a)
Det er 20 elever i hver klasse!!! (Altså et sted uten stykkprisfinansiering).
1A: Gjennomsnitt:
1B: Gjennomsnitt:
Gjennomsnittet i 1A er 3,4 , og i 1B er det 3,6.
b)
Standardavvik er et mål på spredningen i datamaterialet. Vi er ikke bedt om å regne ut standardvviket, bare begrunne i hvilken klasse det er størst. Dersom mange observasjoner ligger langt fra gjennomsnittet er standardavviket stort. I klasse 1A ser vi at det er mange som har karakter 1 og 2, og 5 og 6. Det er karakterer som ligger langt fra gjennomsnittet på 3,4. Det er faktisk bare tre elever som ligger i det området. I klasse 1B er det 11 elever som ligger rundt gjennomsnittet.
Standardavviket er derfor størst i 1A.
c)
| Karakter | Antall (frekvens) A | Kummulativ A | Antall(frekvens) B | Kummulativ B |
| 1 | 5 | 5 | 1 | 1 |
| 2 | 4 | 9 | 3 | 4 |
| 3 | 2 | 11 | 5 | 9 |
| 4 | 1 | 12 | 6 | 15 |
| 5 | 3 | 15 | 4 | 19 |
| 6 | 5 | 20 | 1 | 20 |
Den kummulative frekvens for 3 i 1A er 11. Det betyr at 11 personer i klassen har 3 eller dårligere. Den kummulative frekvensen i 1B er 9.
d)
Den relative frekvensen for 6 i 1A er
Den relative frekvensen for 6 i 1B er
Oppgave 10
a)
Det er fire markante temperaturfall på vannet, derfor er det fire pesoner som dusjer, dersom de dusjer en og en.
b)
Den lengste dusjperioden er på ca. 12,5 minutter. I den perioden faller temperaturen 4 grader. Den siste som dusjer, bruker 10 minutter, men da er temperaturfallet over 6 grader ( ikke en del av spørsmålet, men en interesant observasjon).
c)
Kl. 7:10 er temperaturen 56 grader. Kl 7:30 er den 58 grader. Det betyr at den stiger en grad på 10 min. Den skal opp til 70 grader, det er 12 grader fra hva den var 7:30. Den bruker da 120 minutter på det. Temperaturen er 70 grader to timer etter 7:30, altså 9:30.
DEL TO
Oppgave 1
Oppgave 2
a)
b)
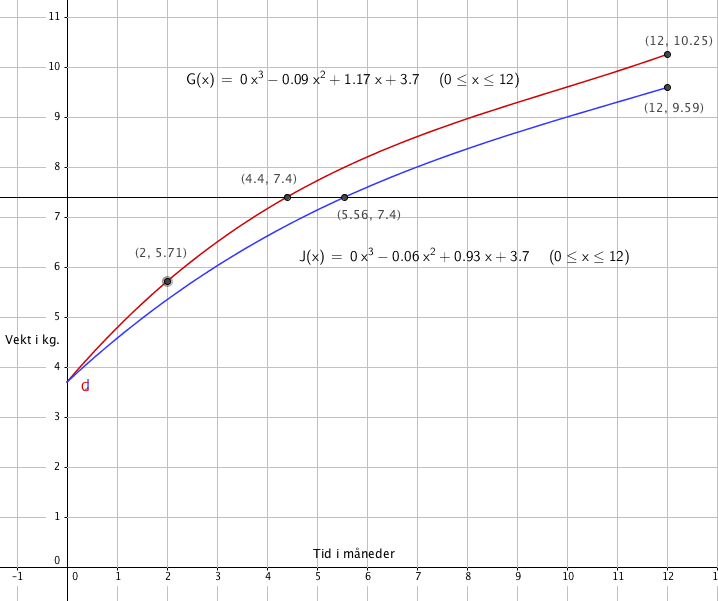
Geir la på seg:
Janne la på seg:
c)
Fra figuren i a ser man at det går ca 4,5 måneder før vekten til Geir er dobblet, og ca. 5,5 før det samme skjer med Janne.
d)
Den gjennomsnittligge månedlige veksten er 0,55 kilogram per måned det første året.
Den gjennomsnittlige veksten de første to månedene er 1 kg per måned.
Oppgave 3
a)
b)
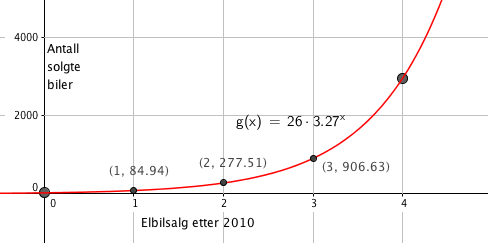
Vekstfaktoren er 3,27. Da er den årlige prosentvise økningen 227%
c)
Modellen er ikke god. Den estimerer for lave salgstall i 2011-2013 (se figur i a), og så urealistisk høye salgstall etter 2014.
Oppgave 4
Oppgave 5
Oppgave 6
a)
b)
c)
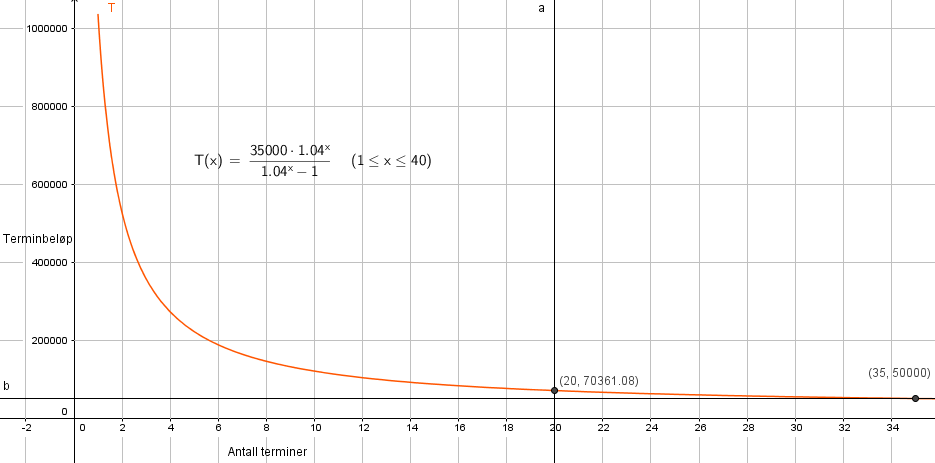
Fra figuren i b ser man at 20 terminer gir et terminbeløp i overkant av 70 000 kroner.
d)
Fra figuren i b ser man at et terminbeløp på 50 000 kroner, gir 35 terminer.
Oppgave 7
a)
Man ser at i det første kvadratet er arealet av det sorte kvadratet lik 1. I den andre kvadratet er arealet av et sort kvadrat
Figur fire:
b)
Se oppgave a.
c)
Figuene er
1, 2, 3.
Kvadratet av disse er:
1, 4, 9.
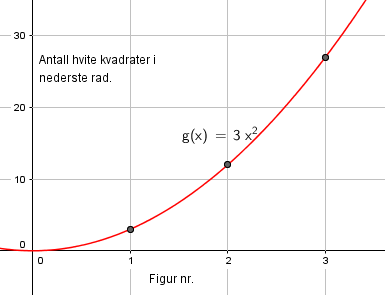
Antall hvite kvadrater på nederste rad er:
3, 12, 27.
Man observerer at kvadratet av figurnummeret må multipliseres med 3 for å få antall hvite kvadrater på nederste rad:
Løst ved regresjon på Geogebra:
d)
Det totale antall hvite kvadrater er:
Antall kvadrater minus antall svarte kvadrater, som er