S1 2015 vår LØSNING

Diskusjon av denne oppgaven på matteprat

Vurderingsskjema

Sensorveiledning

Løsning laget av matteprat-bruker LektorH

Oppgave 1

a)

$2x^2-6x+4=0 \\ x= \frac{6 \pm \sqrt{36 -4 \cdot 2 \cdot 4}}{2 \cdot 2} \\ x= \frac{6 \pm 2}{4} \\ x=1 \vee x= 2$

b)

$2lgx - lg2 = lg(4-x) \\ lg{ \frac{x^2}{2}} = lg(4-x) \\ 10^{ lg{ \frac{x^2}{2}}} = 10^{lg(4-x)} \\ \frac{x^2}{2} = 4-x \\ x^2+2x-8=0 \\ x= \frac{-2 \pm \sqrt{4-4 \cdot 1 \cdot (-8)}}{2} \\ x= \frac{-2 \pm 6}{2} \\ x= -4 \vee x =2$

Likningen inneholder lgx, så alle negative løsninger må forkastes.

Dvs. x = 2. Ved å sette prøve på svaret ser man at begge sider gir lg2.

Oppgave 2

a)

$PC + CB = 30 = x + y$ Det er like langt fra B til P, om C og om A, derav første likning.

$(10+x)^2+400 = y^2$ er pytagoras anvendt på trekanten ABC.

b)

<math> \left[ \begin{align*} x+y=30\\ (10+x)^2+400 = y^2 \end{align*}\right] </math>

<math> \left[ \begin{align*} x=30 - y \\ (10+30-y)^2+400 = y^2 \end{align*}\right] </math>

<math> \left[ \begin{align*} x=30 - y \\ (1600 -80y +y^2 +400 = y^2 \end{align*}\right] </math>

Den nederste likningen gir: 80y = 2000, dvs. y = 25

$x = 5 \vee y = 25$

Oppgave 3

a)

$(a+1)^2 - 2(a-1)(a+1) + (a-1)^2 = \\ a^2+2a+1 -2(a^2-1) +a^2 -2a+1=\\ a^2 +2a+1-2a^2+2+a^2-2a+1=\\ 4$

b)

$\frac{(2a^2)^{-1}(3b)^2}{(3a^2b^{-1})^2} \\ \frac{9b^2b^2}{18a^6}= \\ \frac{b^4}{2a^6}$

Oppgave 4

a)

$f(x)= x^3 -6x^2+9x-4 \quad D_f = \R \\ f´(x) = 3x^2-12x+9$

b)

Setter den deriverte lik null for å finne ekstremalpunkter:

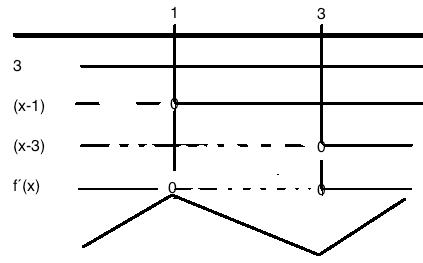
$f´(x) = 0\\ 3x^2-12x+9 =0 \\x = \frac{4 \pm \sqrt{16-12}}{2} \\ x=1 \vee x= 3 $

Faktorisert:

$f´(x)= 3(x-1)(x-3)$

Maksimumspunkt: $f(1)= 1-6+9-4 = 0$. dvs. (1,0).

Minimumspunkt: $f(3)= 27-54+27-4 =-4$. dvs. (3, -4).

c)

Likning til tangenten til grafen i (0, f(0)):

f(0) = -4

f´(0) = 9

$ y= ax+b \\ y= 9x+b \\ -4 = 9 \cdot 0 +b \\ b=-4 \\ y= 9x-4$

d)

Den deriverte til den andre tangenten må være 9.

$f´(x)=9 \\ x= 0 \vee x =4$

Oppgave 5

a)

b)

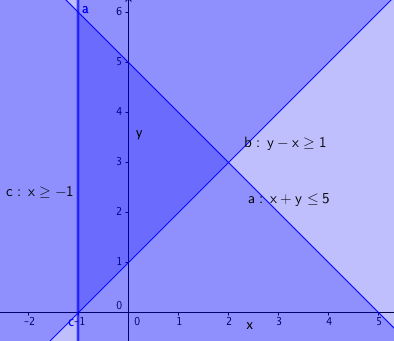
Sjekker hjørnene i trekanten (-1, 0), -1, 6) og (2, 3)

$3x+2y \\ 3 \cdot (-1) +0 = -3 \\ 3 \cdot (-1) + 2 \cdot 6= 9 \\ 3 \cdot 2 + 2 \cdot 3 = 12$

Uttrykket blir størst i punktet (2, 3)

Oppgave 6

a)

$K(x)= 0,25x^2+100x + 5000 \quad x \in [0, 400]$

Inntekt er : $I(x) = 200x$

Overskudd = Inntekt - Kostnad:

$O(x)= I(x)-K(x) \\ O(x)= 200x- 0,25x^2-100x-5000 \\ O(x)= -0,25x^2 + 100x - 5000$

b)

$O´(x) = -0,5x+100$

Setter den deriverte lik null og får løsningen x = 200.

200 solgte enheter gir størst overskudd.

Oppgave 7

a)

$ P(2 røde)= \frac{ \binom{3}{2} \binom{4}{1}}{ \binom{7}{3}} $

Oppgave 2

a)

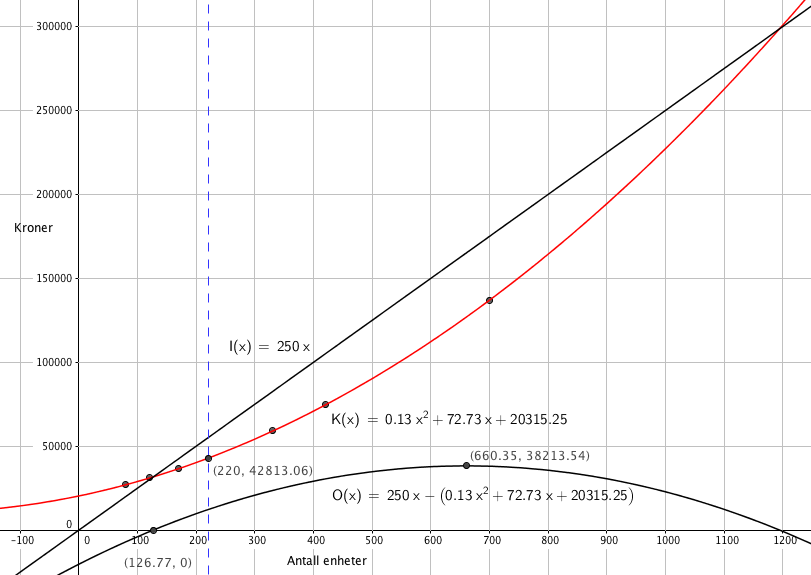
En god modell er $K(x)=0,13x^2+72,73x+20315$

Kostnadene ved å produsere 220 enheter er 48.813 kroner.

b)

Fra figur i a:

For å få overskudd må bedriften produsere og selge 127 eneheter.

c)

Fra figur i a:

Størst overskudd ved 660 enheter, da er overskuddet 38.213,50 kr.

Oppgave 3

a)

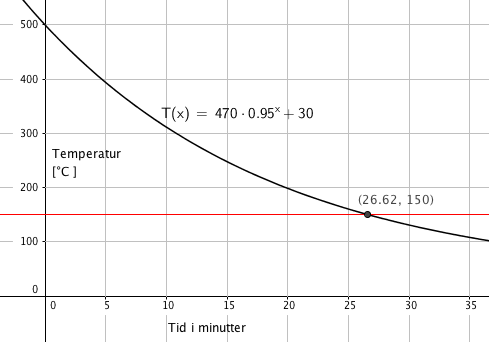
Metallet er 500 grader celsius når det blir tatt ut av ovnen, fra figur. Har også at $T(0)= 470+30 = 500$

b)

Smeden har ca 26,5 minutter til å bearbeide metallstykket. Det er varmt i rommet, 30 grader celsius ( konstanledd i funksjonsuttrykk).

Oppgave 4

a)

Areal av eskens bunn: $A= (6-4x)(6-2x) = \\36-12x-24x+8x^2= \\ 8x^2-36x+36 $

Multipliserer så med høyden av esken, x, og får volumet:

$V(x) = A(x) \cdot x= 8x^3-36x^2+36x \quad x \in <0, 1,5>$