2P 2015 vår LØSNING
- Løsningsforslag (pdf) fra joes. Send gjerne en melding hvis du oppdager feil i fasit. På forhånd, takk.
DEL EN
Oppgave 1
Median av seks målinger er gjennommsnittet av måling 3 og 4.
Tre tall er allerede under 7, det betyr at tall nr 3 er 6 (fredag). Det betyr at det må være 8 grader på lørdag, dersom median skal bli 7, fordi 8 + 6 = 14, som delt på to er 7.
Oppgave 2
$x \cdot 0,8= 240 \\ x= \frac{240}{0,8} \\ x= 300$
Når noe settes ned med 20% er vekstfaktoren 0,8. Pris før nedsettelse var derfor 300 kroner.
Oppgave 3
a)
En million er 1 000 000. En milliard er 1000 millioner. 14 milliarder blir da:
$14 \cdot 1000 \cdot 1000000 = 1,4 \cdot 10^{10}$år.
b)
$1,4 \cdot 10^{10} \cdot 3,2 \cdot 10^7 = 4,48 \cdot 10^{17}$ sekunder gammelt.
Oppgave 4
a)
$\frac {3^2-2^3}{2^0 \cdot 4} = \frac{9-8}{4} = \frac 14$
b)
$\frac{(6a)^2 \cdot b^2}{9a \cdot b^{-2}} \\= \frac{6^2a^2b^2}{9ab^{-2}} \\= \frac{36}{9}a^{2-1}b^{2-(-2)} \\ = 4ab^4$
Oppgave 5
a)
En lineær modell er på formen
f(x) = ax + b
Nedgangen er på 60 elever på 10 år, dvs. 6 elever per år. Vi får da:
f(x) = -6x + 1400,
der x er antall år regnet fra 10 år tilbake. Dvs. x=10 er nå.
b)
$ g(x) = 1340 \cdot 0.995^x$
1340 er antall elever nå. 0,995 er vekstfaktoren når noe minker med 0,5%. x er antall år fra nå.
Oppgave 6
a)
b)
c)
| Alder | frekvens | relativ frekvens | kumulativ frekvens |
| [ 20,30> | 10 | $\frac{1}{10}$ | 10 |
| [30, 40> | 20 | 30 | |
| [40,50> | 30 | 60 | |
| [ 50,70> | 40 | 100 |
Oppgave 7
a)
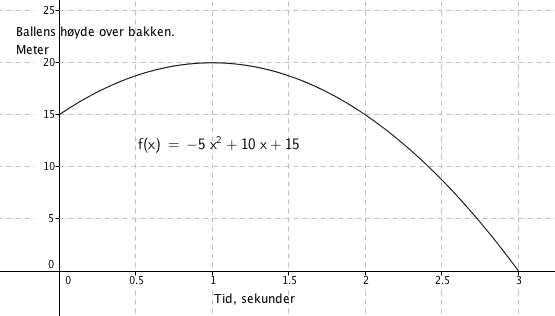
| h | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| h(t) | 15 | 18,75 | 20 | 18,75 | 15 | 8,75 | 0 |
b)
c)
h(0) er i kastøyeblikket. Karl står på en balkong 15 meter over bakken.
h(3), ballen lander. Hele ballens svev tok tre sekunder.
Oppgave 8
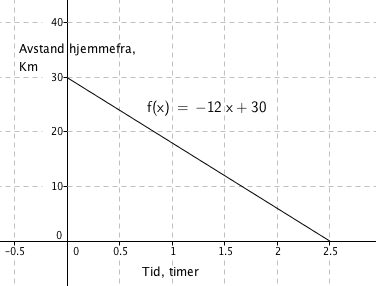
Han starter 30 km hjemmefra og sykler mot hjemmet med konstant fart. Han kommer nærmere og nærmere og er hjemme etter to og en halv time. Funksjonenover viser avstand fra hjemmet f, som funksjon av tiden i timer, x.