S1 2013 høst LØSNING

Oppgave 1

$f(x)= 3x^2+3x+1 \qquad D_f = \R \\f'(x)= 6x-3 \\f´(2)= 6 \cdot 2 -3 = 9$

Oppgave 2

a)

$x(x+5)-10 =4 \\ x^2+5x-14=0 \\ x= \frac{-5\pm \sqrt{25+56}}{2} \\x= -7 \vee x=2$

b)

$10^{3x} -100000 =0 \\ 10^{3x} = 10^5 \\ 3x=5 \\ x=\frac 53$

Oppgave 3

<math> \left[ \begin{align*} y = x^2+2\\ y+x^2=4 \end{align*}\right] </math>

<math>\left[ \begin{align*} x^2+2+x^2-4=0 \\ 2(x^2-1) =0 \\ x=-1 \vee x=1\end{align*}\right] </math>

$x=-1 \Rightarrow y=3 \\ x=1 \Rightarrow y=3 \\ (-1,3 ) \wedge (1,3)$

Oppgave 4

a)

$v=v_0+at \\t = \frac{v-v_0}{a}$

b)

$t = \frac{v-v_0}{a} \\ t = \frac{25-1}{3}=8 $

Oppgave 5

a)

$ \frac{9^2a^2b^3}{(3ab^2)^2} \\ =\frac{3^4a^2b^3}{3^2a^2b^6} \\ = 3^{4-2} \cdot a^{2-2} \cdot b^{3-6} \\ = 3^2b^{-3} \\ = \frac{9}{b^3} $

b)

$\lg (\frac{a^2}{b^2}) + \lg( \frac {b^2}{a}) + lg (a+b) \\ =\lg a^2 - \lg b^2 + \lg b^2 - \lg a + \lg (a+b) \\= 2\lg a - \lg a + \lg(a+b) \\ = \lg a + \lg (a+b) \\ =lg (a(a+b)) \\ =\lg (a^2+ab)$

Oppgave 6

$x^2+2x \ge x-6 \\ x^2+x-6 \ge 0 \\ x= \frac{1 \pm \sqrt{25}}{2} \\ (x-2)(x+3)\ge 0$

Oppgave 7

<math> \left[ \begin{align*} 21+x = y\\ y+2x = 126 \end{align*}\right] </math>

$ 21+x+2x= 126 \\ 3x= 105 \\ x= 35 \\ y= x+21 = 56 \\ x= 35 \wedge y= 56 $

Oppgave 8

$ f(x)=x^3-6x^2 \qquad D_f = \R$

a)

Nullpunkt:

$f(x)= 0 \\ 2x^3 - 6x^2 =0 \\ 2x^2(x-3) =0 \\ x=0 \vee x= 3 \\ f(0) =0 \wedge f(3)= 0$

Nullpunkt i (0, 0) og (3, 0)

b)

Ekstremalpunkt:

$f´(x) = 6x^2-12x \\ f´(x)=0 \\ 6x(x-2)=0 \\ x= 0 \vee x=2 \\ f(0) = 0 \wedge f(2)=-8$

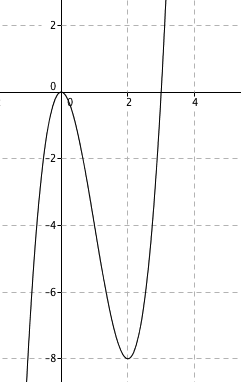
c)

Oppgave 9

$f(0)=-2 \Rightarrow b=2 \\ f(-1) =0 \Rightarrow a=2 $

Vertikal asymptote: $x=1 \Rightarrow c=1$

Funksjonen blir da:

$f(x)= \frac{ax+b}{cx -1} = \frac{2x+2}{x-1}$