R1 2011 høst LØSNING
DEL EN
Oppgave 1:
a
1)
2)
3)
b
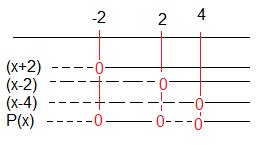
1)
Siden P(2) = 0 er x=2 et nullpunkt.
2)
3)
c
y må være mindre enn a fordi man ikke kan ta logaritmen til et negativt tall.
d
1)
2)
3)
e)
1)
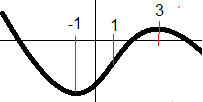
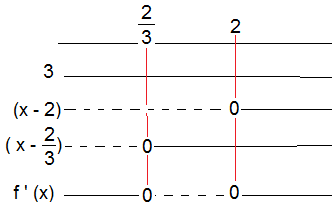
f minker i områdene minus uendelig til -1 og fra 3 til uendelig
f vokser fra -1 til 3.
2)
f har to ekstremalpunkt, et minimumspunkt for x = -1 og et maksimumspunkt for x = 3. Grafen har et vendepunkt for x=1. For verdier mindre enn 1 vender grafen sin hule side opp, og for verdier større enn 1 vender den sin hule side ned.
3)
f)
g)
1)
Vinkel ADB er en pereferivinkel og skjærer over samme bue som AOB. Vinkel ADB er defor
2)
Vinkel DBE er en pereferivinkel som spenner over samme bue som DOE. Vinkel DBE er derfor
3)
Vinkelsummen i en trekant er 180 grader. I trekanten BCD er vinkel DBC 10 grader. Vinkel BDC er 180 - 30 = 150 grader. Vinkel ACB må da vare lik 20 grader.
DEL TO
Oppgave 2:
a)
Summen under rottegnet i andregradsformelen er null. Det gir sammenfallende løsning for x = 2, hvilket betyr at grafen til f tangerer x-aksen i punktet (2,0)