1T 2011 vår LØSNING

Del 1

Oppgave 1

a)

1) <tex>36 200 000 = 3.62 \cdot 10^7</tex>

2) <tex>0.034 \cdot 10^{-2} = 3.4 \cdot 10^{-4}</tex>

b)

<tex>x^2 + 6x = 16 \quad \Leftrightarrow \quad x^2 + 6x - 16 = 0</tex>

Ved fullstendig kvadrat:

<tex>\begin{align} x^2 + 6x - 16 &= x^2 + 6x + \Big( \frac{6}{2} \Big)^2 - 16 - \Big( \frac{6}{2} \Big)^2 \\ &= x^2 + 6x + 9 - 25 \\ &= (x+3)^2-5^2 \\ &= (x + 3 - 5)(x + 3 + 5) \\ &= (x - 2)(x + 8) \\ &= 0 \end{align} </tex>

<tex>x = 2 \quad \vee \quad x = -8</tex>

Eller med abc-formelen:

<tex>x = \frac{-6 \pm \sqrt{6^2 - 4\cdot 1 \cdot (-16)} }{2 \cdot 1} = \frac{-6 \pm \sqrt{100}}{2} = -3 \pm 5</tex>

<tex>x = 2 \quad \vee \quad x = -8</tex>

c)

Begynner med å faktorisere uttrykket:

<tex>x^2-x<0 \Leftrightarrow x(x-1)<0 </tex>

Tegner så fortegnsskjema:

d)

1) E

2) C

3) J

4) B

5) G

6) H

e)

<tex>\text{lg}(2x - 1) = 2</tex>

<tex>2x - 1 = 10^2</tex>

<tex>2x = 101</tex>

<tex>x = \frac{101}{2}</tex>

f)

1)

2)

Oppgave 2

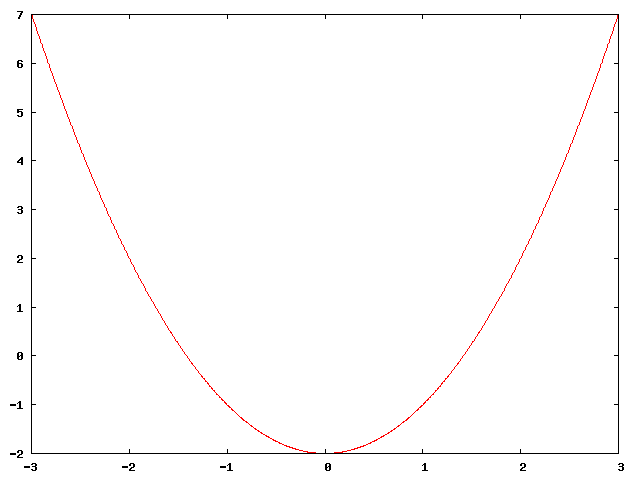
a)

b)

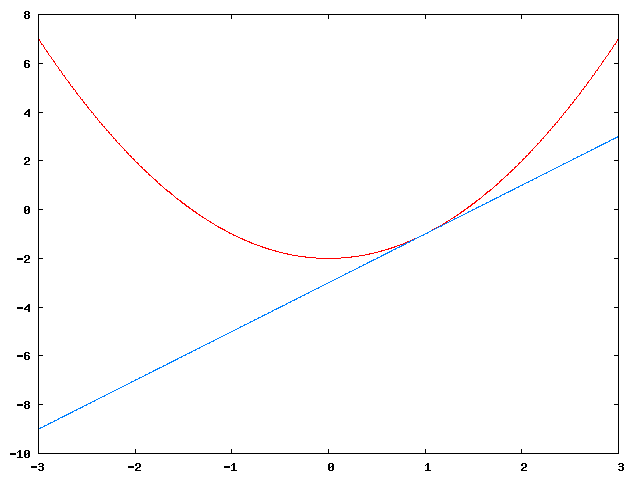
Sekanten er gitt ved

<tex>\begin{align}S(x) &= f(0) + \frac{f(2) - f(0)}{2-0}(x-0) \\ &= -2 + \frac{(2^2-2)-(-2)}{2}x \\ &= 2x-2\end{align}</tex>

c)

Tangenten er gitt ved

<tex>\begin{align} T(x) &=f(1) + f^{\prime}(1)(x-1) \\ &= 1^2-2 + 2(x-1) \\ &= 2x - 3 \end{align} </tex>

Der det er brukt at <tex>f^{\prime}(x) = 2x</tex>.