2P 2024 Vår LØSNING
Diskusjon av oppgaven på matteprat
Løysing laga av Torodd F. Ottestad
DEL 1
Oppgave 1
Gjennomsnitt: legger sammen alle tallene og deler på antall tall.
$\frac{1+ 3+ 4+ 0+ 4+ 5+ 2+ 7+ 12+ 2}{10}=\frac{40}{10}=4$
Gjennomsnittet er 4 timer på sosiale medier per dag.
Median: ordner tallene i stigende rekkefølge og finner gjennomsnittet av de to midterste tallene.
$0, 1, 2, 2, 3, 4, 4, 5, 7, 12$
De to midterste tallene er 3 og 4, og gjennomsnittet av disse er 3,5.
Medianen er 3,5 timer på sosiale medier per dag.
Oppgave 2
Prisen på varen følger konsumprisindeksen. Dersom varen kostet 1000 kr i 2015, ville den kostet 1296 kr i 2023. Siden varen kostet 500 kr i 2015 (altså halvparten av 1000), vil varen koste 648 kr (halvparten av 1296 kr) i 2023.
Oppgave 3
Målestokk angir hvor mange cm i virkeligheten én cm på kartet viser.
2 cm på Astrids kart tilsvarer 300 m i virkeligheten, som vil si at 1 cm på Astrids kart tilsvarer 150 m i virkeligheten.
150 m = 15 000 cm, altså er målestokken 1:15000.
Oppgave 4
x = pris for én ispinne
y = pris for én boks med mineralvann
Lager et likningssystem:
Likning I $\quad 30x+30y=900$
Likning II $\quad y=x+6$
Bruker innsettingsmetoden og setter inn verdien for y fra likning II, inn i likning I.
$30x+30(x+6)=900$
$30x+30x+180=900$
$60x=900-180$
$x=\frac{720}{60}$
$x = 12$
Setter inn verdien for x inn i likning II:
$y = x+6$
$y = 12+6= 18$
En ispinne kostet 12 kroner, og en boks med mineralvann kostet 18 kroner.
Oppgave 5
Pris per bagett i det første tilbudet: 32 kr / 2 = 16 kr
Pris per bagett i det andre tilbudet: 48 kr / 4 = 12 kr
Prisforskjell per bagett: 16 kr - 12 kr = 4 kr
Prosent forskjell i pris per bagett, sammenlignet med den dyreste prisen: $\frac{4}{16}\cdot 100\%=\frac{1}{4}\cdot 100\%=25\%$
Det blir 25 % billigere per bagett å kjøpe fire bagetter, enn å kjøpe to bagetter.
DEL 2
Oppgave 1
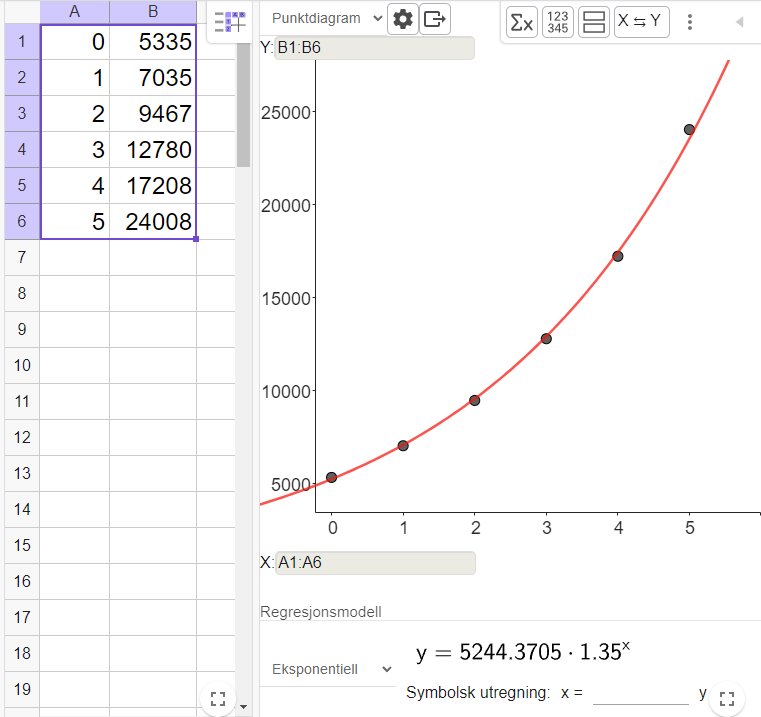
Tuva kan ha brukt eksponentiell regresjonsanalyse, som vist under i Geogebra.
Her er vekstfaktoren 1,35, som betyr en månedlig vekst på 35 % følgere.