R1 2023 Høst LØSNING
Diskusjon av oppgaven på Matteprat
Løsningsforslag laget av Realfagsportalen
Løsning laget av Sindre Sogge Heggen
Løsningsforslag laget av Farhan Omar
Videoløsning av hele eksamenssettet av UDL.no
Videoløsning del 1 av Lektor Lainz (Reabel)
REA 3056
Del 1
Oppgave 1
$f(x) = x^2 \cdot ln(x)$
$f'(x) = 2x \cdot ln(x) + x^2 \cdot \frac1x = x(ln(x)+1)$
Oppgave 2
$2 \ln e^3 = 2\cdot 3 \ln e =6$
3 lg(70) Vi vet at lg 70 er mellom 1 og 2 fordi lg 10 = 1 og lg100= 2, så uttrykket er mellom 3 og 6. Vi kan omforme:
$3lg(70) = 3 lg(10 \cdot 7) = 3 (lg10 + lg 7)= 3 + 3lg 7$
$e^{3\ln2} = e^{{\ln2}^3} = 2^3 = 8$
I stigende rekkefølge:
$3 \lg(70), \quad 2 \ln e^3, \quad e^{3 \ln 2}$
Oppgave 3
a)
$\overrightarrow{AB} = [2-(-3), -2-(-1)]= [5,-1]\quad $ lengde $\sqrt{26}$
$\overrightarrow{BC}= [5-2, 2-(-2)] = [3, 4] \quad$ lengde $\sqrt{9+16} = 5$
$\overrightarrow {CA} = [-3-5), -1-2] = [-8, -3] \quad$ lengde $\sqrt {73}$
Sidekanten BC er kortest.
b)
Dersom skalarproduktet mellom vektorene er null, er vinkelen mellom dem 90 grader.
$\overrightarrow{AB} \cdot \overrightarrow{BC} = [5,-1] \cdot [3,4] = 15- 4 = 11$
$\overrightarrow{BC} \cdot \overrightarrow{CA} = [3,4] \cdot [-8,-3] = -24-12 = -36$
$\overrightarrow{CA} \cdot \overrightarrow{AB} = [-8, -3] \cdot [5, -1] = -40+ 3 = -37$
Ingen av vinklene i trekanten er 90 grader.
Oppgave 4
a)
b)
Del to
Oppgave 1
a)
b)
c)
Oppgave 2
a)
$f(k) = k^2+(2-k)k = 2k$
$\lim\limits_{ x \to k^+} (x^2 + (2-k)x) = f(k) = 2k$
$\lim\limits_{ x \to k^-} (-x^2 + (2+k)x) = f(k) = 2k$
Funksjonene er kontinuerlig.
b)
c)
Oppgave 3
a)
b)
c)
Oppgave 4
a)
b)
Vi setter opp et uttrykk for arealet av boksens overflate. Vi kaller sidene i grunnflaten for x og høyden for h:
$x^2 + 4xh = 120$
Bruker denne sammenhengen til å finne et uttrykk for h: $h = \frac{120-x^2}{4x}$
Finner så et uttrykk for volumet:
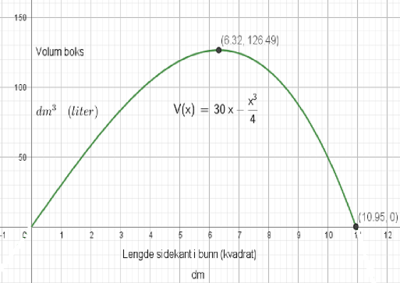
$V(x)= x^2 \cdot h = x^2 \cdot \frac{120-x^2}{4x} = 30x - \frac{x^3}{4}$
Det maksimale volumet boksen kan få er 126,5 liter. Da er sidekantene i bunnen ca. 63 cm.
c)
Her følger vi samme metodikk som i b, men nå finner vi et uttrykk for h ved å ta utgangspunkt i volumet: $x^2\cdot h = 80$
Vi finner h uttrykt ved x: $h= \frac{80}{x^2}$
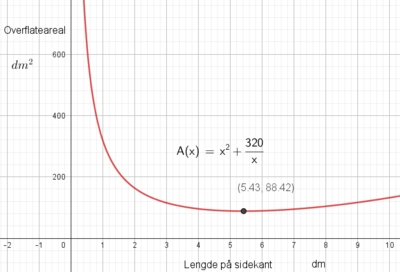
Overflatearealet kan da uttrykkes som : $A(x) = x^2 + 4xh = x^2+ 4x \cdot \frac{80}{x^2} = x^2 + \frac{320}{x}$
Oppgave 5
a)
b)
c)
Oppgave 6
a)
$f(x)= x^2 + 3x + 1$
$f'(x) = 2x + 3$
$f'(c) = \frac{f(b) - f(a)}{b-a} = \frac{f(3)- f(1)}{3-1} = \frac {(9+9+1) - (1+3+1)}{2} = 7$
$f'(c) = 2c+3 = 7 $
$c = 2$