1T 2022 høst LK20 LØSNING
Diskusjon av oppgaven på matteprat
DEL EN
Oppgave 1
hvilket skulle vises.
Oppgave 2
a)
Nullpunktene til f(x) er x=-4, x=2 og x=4.
Disse nullpunktene passer best med graf A.
b)
Dette er samme uttrykk som f(x) i oppgave a). Vi ser av tegninga til graf A, at f(x)>0 i intervallene
Oppgave 3
a)
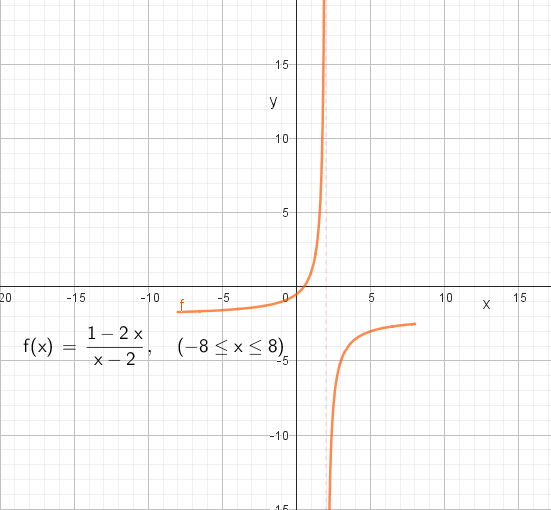
Lars ønsker å bruke programmet til å skrive ut x verdier med tilhørende funksjonsverdi, fra x=8 til x=-8. Det går bra helt til x=2, da prøver programmet å dele på null, og gir feilmelding.
b)
Lars kan legge til en if-setning inni while-løkka, som dersom x=2, skriver ut at funksjonsverdien ikke er definert. For eksempel fra linje 7, inni while-løkka:
if x == 2:
else:
x=x-1
c)
Bruk en verditabell til å tegne punktene inn i et koordinatsystem (for hånd). Grafen til funksjonen skal se slik ut:
Oppgave 4
Den deriverte til en parabel vil være en rett linje.
Vi er på jakt etter likningen y = ax + b og finner først a:
Så kan vi bruke punktet( 8, -11) og får
Desom vi bruker det andre punktet:
Likningen til den deriverte blir y = -2x + 5
DEL TO
Oppgave 1
a)
Da er x null, så temperaturen blir da 3,5 + 34,5 = 38 grader celsius når strømmen slåes av.
Se linje 2 i CAS, T(0) er lik 38.
b)
Se linje 3 i CAS. Det vil ta ca. 5,3 timer før temperaturen er under 20 grader.
c)
Se linje 4 i CAS. Stigningstallet er ca. -3.68 grader per time, mellom 0 og 4 timer etter at strømmen blir slått av. Det vil si at temperaturen gjennomsnittlig synker med 3,68 grader per time i dette intervallet.
d)
Se linje 5 og 6 i CAS. Temperaturen synker ikke med mer enn 5 grader per time, etter at strømmen har blitt slått av. (Modellen T(x) gjelder kun for
Den mest ekstreme momentane endringen er i starten, rett etter at strømmen blir slått av. Da er endringen - 4,8
e)
3,5 er temperaturen til omgivelsene.
Oppgave 2
Antalls treroms er x og antall toroms er y.
x + y = 40
3x+ 2y = 90
Multipliserer første likning med -2. Legger så sammen likningene og får
x = 10. Da er y= 30.
Det er altså 10 treroms og 30 toroms i bygården.