S1 2020 høst LØSNING
Diskusjon av denne oppgaven på matteprat
Løsningsforslag laget av Marius Nilsen ved Bergen Private Gymnas
DEL 1
Oppgave 1
a)
b)
c)
Oppgave 2
a)
b)
Oppgave 3
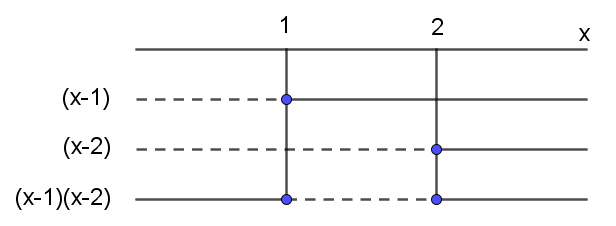
Nullpunkter:
Oppgave 4
La
Norge tok 11 gullmedaljer i vinter-OL i 2014.
Oppgave 5
a)
Sannsynligheten for at Mia må ta oppvasken dersom de følger dette forslaget er
b)
La
Setter
Velger den positive løsningen,
Det må ligge flere enn 5 røde kuler i krukken, dersom sannsynligheten for at de to kulene som trekkes har ulik farge, er mindre enn 50 %.
Oppgave 6
Vi har
Oppgave 7
a)
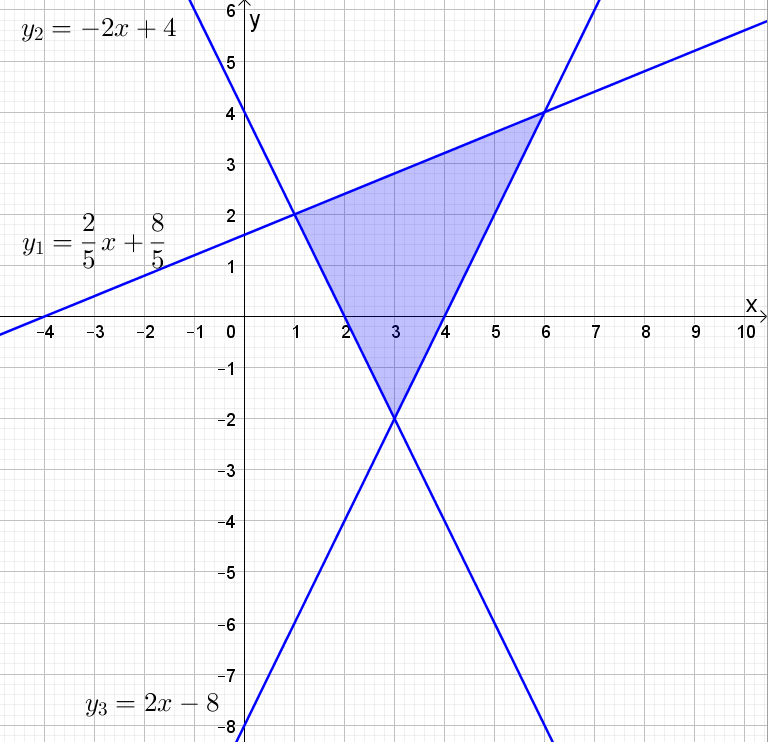
Skriver om ulikhetene på formen y=ax+b. Tegner inn disse linjene i et koordinatsystem (du må gjøre det for hånd).
b)
Regner ut verdien til uttrykket
Hjørnet (1,2):
Hjørnet (3,-2):
Hjørnet (6,4):
Uttrykket
Oppgave 8
a)
Gjennomsnittlig vekstfart:
Den gjennomsnittlige vekstfarten til g i intervallet
b)
c)
Setter
Oppgave 9
a)
Vi har omkretsen til rektangelet
b)
Vi trenger et uttrykk for radiusen til sylinderen. Vi har omkretsen til sylinderen
Volumet av en sylinder:
c)
Setter
Vi kan ikke ha en omkrets x=0, så vi må ha omkretsen x=32 for at volumet av sylinderen skal bli størst mulig.
Notat: andregradsleddet til den deriverte har negativt fortegn, så den deriverte er en andregradsfunksjon som vender den hule siden ned. Det vil si at V'(x) er positiv i intervallet
DEL 2
a)
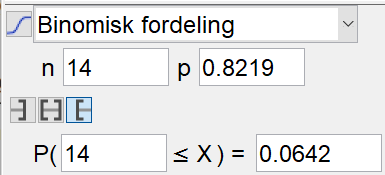
Sannsynligheten for at det er sol en tilfeldig dag på Gran Canaria er
Bruker sannsynlighetskalkulatoren i Geogebra og velger binomisk fordeling. Velger n=14 og p=0,8219, som gir
Agnete har antatt en binomisk fordeling av soldager. Det innebærer at:
b)
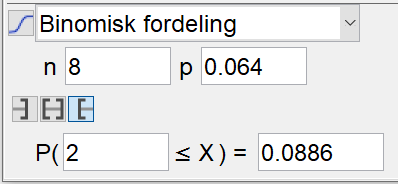
Bruker sannsynlighetskalkulatoren i Geogebra, og velger igjen en binomisk fordeling. Velger n = 8 (antall ferier), og p = 0,064 (sannsynligheten for bare soldager i en ferie). Finner
Det er 8,86 % sannsynlighet for at familien opplever bare soldager på minst 2 av sine 8 ferier på Gran Canaria.
c)
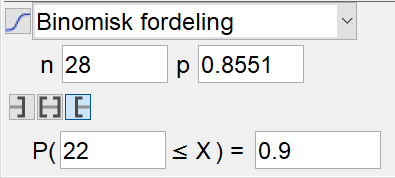
Bruker sannsynlighetskalkulatoren i Geogebra, og velger binomisk fordeling. Velger n = 28 (4 x 7 dager), og prøver meg frem til en sannsynlighet som gir
Det må minst være i gjennomsnitt 313 soldager i året på dette stedet, for at påstanden fra reisebyrået skal være sann.