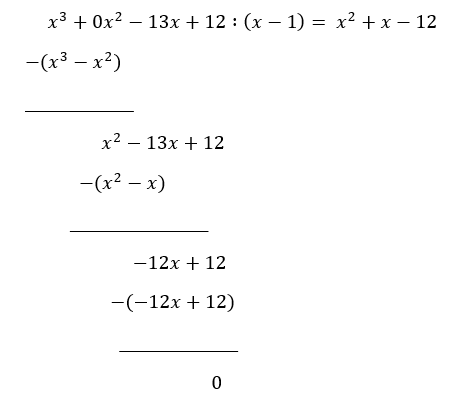R1 2018 vår LØSNING
Diskusjon av denne oppgaven på matteprat
Løsningsforslag (pdf) (open source, meld fra om forbedringer eller feil her)
Løsningsforslag av LektorNilsen (pdf)
Løsning som video av Lektor Håkon Raustøl
DEL 1
Oppgave 1
a)
$f(x)=x^4-x+2$
$f'(x)=4x^3-1$
b)
$g(x)=x^3\cdot ln(x)$
$g'(x)=3x^2\cdot ln(x) + x^3 \cdot \frac{1}{x} = 3x^2ln(x)+x^2$
c)
$h(x)=e^{2x^2+x}$
$h'(x)=(4x+1)e^{2x^2+x}$
Oppgave 2
a)
$\frac{1}{2x-2}+\frac{2}{x-3}-\frac{x-2}{x^2-4x+3} \\ = \frac{1\cdot \color{blue}{(x-3)}}{2(x-1)\color{blue}{(x-3)}}+\frac{2\cdot \color{red}{2(x-1)}}{\color{red}{2(x-1)}(x-3)}-\frac{\color{orange}{2}(x-2)}{\color{orange}{2}(x-1)(x-3)} \\ =\frac{ (x-3) + (4x-4) - (2x-4)}{2(x-1)(x-3)} \\ = \frac{x+4x-2x -3-4+4}{2(x-1)(x-3)} \\ = \frac{3x-3}{2(x-1)(x-3)} \\ = \frac{3(x-1)}{2(x-1)(x-3)} \\ = \frac{3}{2(x-3)} \\ = \frac{3}{2x-6}$
b)
$2ln(x\cdot y^3)-\frac{1}{2}ln(\frac{x^4}{y^2}) \\ = 2(ln(x)+ln(y^3))-\frac{1}{2}(ln(x^4)-ln(y^2)) \\= 2(ln(x)+3ln(y))-\frac{1}{2}(4ln(x)-2ln(y)) \\= 2ln(x)+6ln(y)-2ln(x)+ln(y) \\= 7ln(y)$
Oppgave 3
Vi har punktene A(-2,-1), B(-1, -3), C(3, -1) og D(t,t^2+2) der $t\in R$.
a)
$\vec{AB} = [-1-(-2), -3-(-1)] = [1, -2]$
$\vec{BC} = [3-(-1), -1-(-3)] = [4, 2]$
b)
$[1,-2]\cdot[4,2] = 1\cdot 4 + (-2)\cdot 2 = 4-4 = 0$
Skalarproduktet av $\vec{AB}$ og $\vec{BC}$ er 0, og vi har derfor $\vec{AB}\perp\vec{BC}$
c)
$\vec{CD}=[t-3, t^2+2-(-1)] = [t-3, t^2+3]$
Dersom $\vec{CD}\| \vec{AB}$, så er $\vec{CD} = k\cdot\vec{AB}$
$[t-3,t^2+3]=k\cdot[1,-2]$
Vi får likningssettet:
$I \quad t-3 = k$
$II \quad t^2+3=-2k$
$II \quad t^2+3 = -2 (t-3) \\ \quad t^2 + 3 = -2t+6 \\ \quad t^2 + 2t -3 = 0 \\ \quad (t+3)(t-1) = 0 \\ \quad t = -3 \vee t = 1$
$\vec{CD}\| \vec{AB}$ når $ t = -3 \vee t = 1$.
Oppgave 4
Vi har $f(x)=x^3+k\cdot x + 12$
a)
Dersom $f(x):(x-1)$ skal gå opp, er x=1 et nullpunkt.
$f(1)=0 \\ 1^3+k\cdot 1 + 12 = 0 \\ k+13 = 0 \\ k=-13$
b)
Vi har nå $f(x)=x^3-13x+12$
Utfører polynomdivisjonen:
$f(x)=(x^2+x-12)(x-1) = (x-3)(x-1)(x+4)$
c)
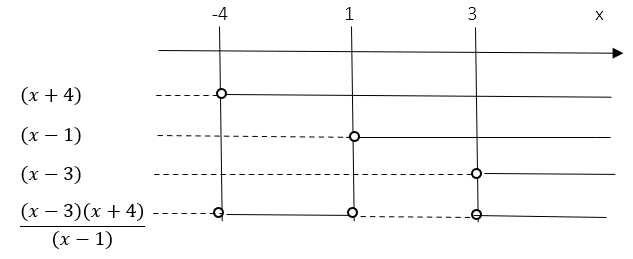
$\frac{x^2+x-12}{x-1} \geq 0 \\ \frac{(x-3)(x+4)}{x-1} \geq 0$
$\frac{x^2+x-12}{x-1} \geq 0$ nå $x\in [-4,1]\cup [3,\rightarrow \rangle$