S1 2018 vår LØSNING
Løsning laget av mattepratbruker Tommy O.
Løsning laget av LektorNilsen (pdf)
diskusjon av oppgaven på matteprat
DEL1
Oppgave 1
a)
$2x^2-5x+1=x-3 \\ 2x^2-5x-x+1+3 = 0 \\ 2x^2-6x+4=0 \quad |:2 \\ x^2-3x+2=0$
Bruker abc-formelen $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$, $a=1$, $b=-3$, $c=2$.
$x=\frac{-(-3)\pm\sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot1} \\ x=\frac{3\pm\sqrt{1}}{2} \\ x_1=\frac{3-1}{2} \vee x_2=\frac{3+1}{2} \\ x_1=1 \vee x_2=2$
b)
$2lg(x+7)=4 \quad |:2\\ lg(x+7)=2 \\ 10^{lg(x+7)}=10^2 \\ x+7 = 100 \\ x=93$
c)
$3\cdot2^{3x+2}=12\cdot2^6 \quad |:3 \\ 2^{3x+2} = 4\cdot 2^6 \quad |:2^6 \\ \frac{2^{3x+2}}{2^6} = 4 \\ 2^{3x+2-6}=4 \\ 2^{3x-4}=2^2 \\ 3x-4=2 \\ 3x=6 \\ x=2$
Oppgave 2
<math> \left[ \begin{align*} x^2 + 3y = 7 \\ 3x - y = 1 \end{align*}\right] </math>
Løser likning to med hensyn på y:
$3x-y=1 \\ 3x-1=y \\ y=3x-1$
Bruker innsettingsmetoden og erstatter y med 3x-1 i likning én.
$x^2+3(3x-1) = 7 \\ x^2+9x-3-7=0 \\ x^2 +9x-10=0$
Bruker abc-formelen $x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$, $a=1$, $b=9$, $c=-10$.
$x=\frac{-9\pm\sqrt{(9)^2-4\cdot 1 \cdot (-10)}}{2\cdot1} \\ x=\frac{-9\pm\sqrt{121}}{2} \\ x_1=\frac{-9-11}{2} \vee x_2=\frac{-9+11}{2} \\ x_1=-10 \vee x_2=1$
Bruker likning to for å finne tilhørende y-verdier:
$y=3x-1 \\ y_1=3\cdot (-10)-1 \quad \vee \quad y_2=3\cdot 1 - 1 \\ y_1=-31 \quad \vee \quad y_2=2$
Løsning: $x_1=-10 \wedge y_1=-31 \quad \vee \quad x_2=1 \wedge y_2=2 $
Oppgave 3
a)
$(2x-3)^2-2x(2x-6)\\=(2x)^2-2\cdot2x\cdot3+3^2-2x\cdot2x-2x\cdot(-6)\\=4x^2-12x+9-4x^2+12x\\=9$
b)
$lg(2a)+lg(4a)+lg(8a)-lg(16a)\\=lg(\frac{2a\cdot4a\cdot8a}{16a})\\=lg(4a^2)\\=lg(2a)^2\\=2lg(2a)$
c)
$\frac{1}{a}+\frac{1}{b}-\frac{a-b}{ab}\\=\frac{1\cdot b}{a\cdot b}+\frac{1\cdot a}{a\cdot b}-\frac{a-b}{ab}\\=\frac{b}{ab}+\frac{a}{ab}-\frac{a-b}{ab}\\=\frac{b+a-a+b}{ab}\\=\frac{2b}{ab}\\=\frac{2}{a}$
Oppgave 4
Kjenner igjen likningen $x^2-3x+2=0$ fra oppgave 1a). Løsningen var $x_1=1$ og $x_2=2$.
Et andregradsuttrykk $ax^2+bx+c$ med nullpunkter $x_1$ og $x_2$ kan faktoriseres slik: $ax^2+bx+c=a(x-x_1)(x-x_2)$
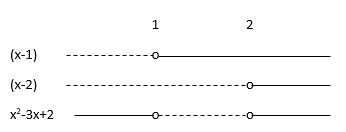
Faktoriserer uttrykket: $x^2-3x+2=(x-1)(x-2)$
Lager fortegnsskjema:
Løsning: $x^2-3x+2\geq0$ når $x\leq1 \wedge x\geq2$
Oppgave 5
a)
b)
Bruker hypergeometrisk sannynlighet, og leser av binomialkoeffisientene i Pascals trekant. (Eksempel: $\binom{7}{3}$ finner du i rad nr.7 og tall nr.3 i raden. Husk å begynne å telle på rad nr.0 og tall nr.0. Hvis du har talt riktig finner du at $\binom{7}{3}=35$).
P(tre blå kuler)=$\frac{\binom{4}{3}\cdot \binom{3}{0}}{\binom{7}{3}}=\frac{4\cdot1}{35}=\frac{4}{35}$
Sannsynligheten for at du trekker 3 blå kuler er $\frac{4}{35}$.
c)
Dersom du skal trekke både røde og blå kuler, må du trekke enten én blå og to røde, eller to blå og én rød.
P(både røde og blå kuler) = P(én blå og to røde)+P(to blå og én rød)
$=\frac{\binom{4}{1}\cdot\binom{3}{2}}{\binom{7}{3}}+\frac{\binom{4}{2}\cdot\binom{3}{1}}{\binom{7}{3}}\\=\frac{4\cdot3}{35}+\frac{6\cdot3}{35}\\=\frac{12+18}{35}\\=\frac{30}{35}\\=\frac{6}{7}$
Sannsynligheten for at du trekker både røde og blå kuler er $\frac{6}{7}$
Oppgave 6
Uttrykker de to siste ulikhetene med hensyn på y:
Ulikhet nr. 3: $x+y\leq 10 \\ y \leq -x+10$
Ulikhet nr. 4: $3x-2y \leq -2 \\ -2y \leq -3x - 2 \quad |:(-2) \\y \geq 1,5x + 1$
NB: husk å snu ulikhetstegnet når du ganger eller deler en ulikhet med et negativt tall.
Vi har nå de fire ulikhetene:
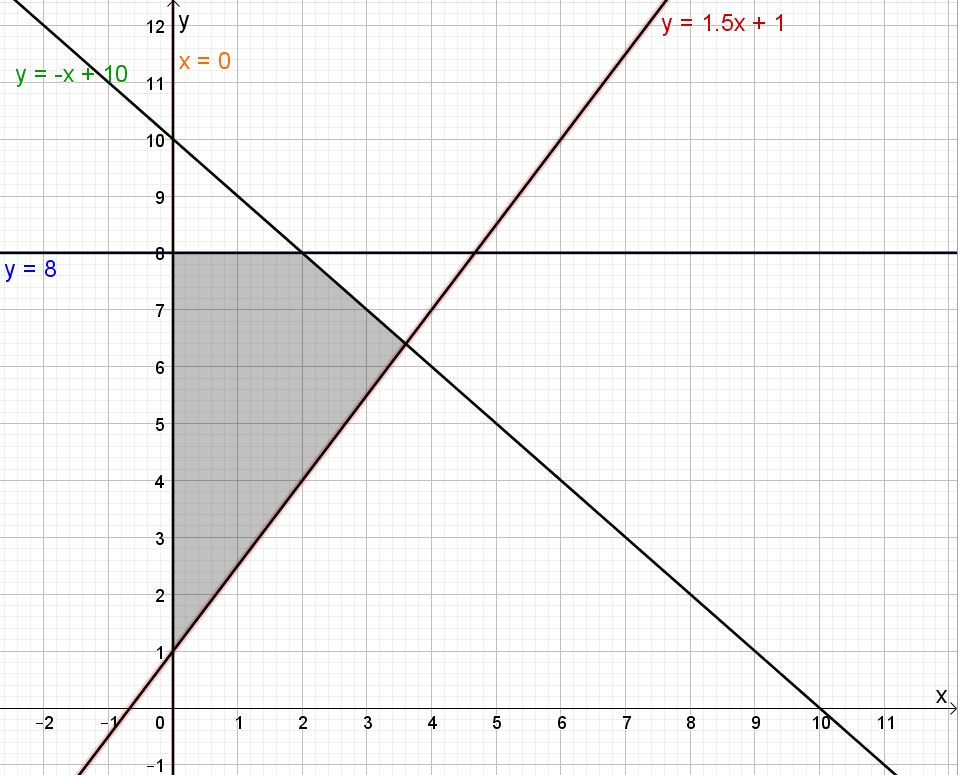
$x\geq0 \\ y\leq 8 \\ y \leq -x+10 \\ y \geq 1,5x + 1$
Tegn de fire linjene $x=0,\,y=8,\,y=-x+10,\,y=1.5x+1$ (for hånd siden det er del 1). Legg godt merke til hvilken vei ulikhetstegnet er i de fire ulikhetene, og skraver området som avgrenses av disse.
Oppgave 7
a)
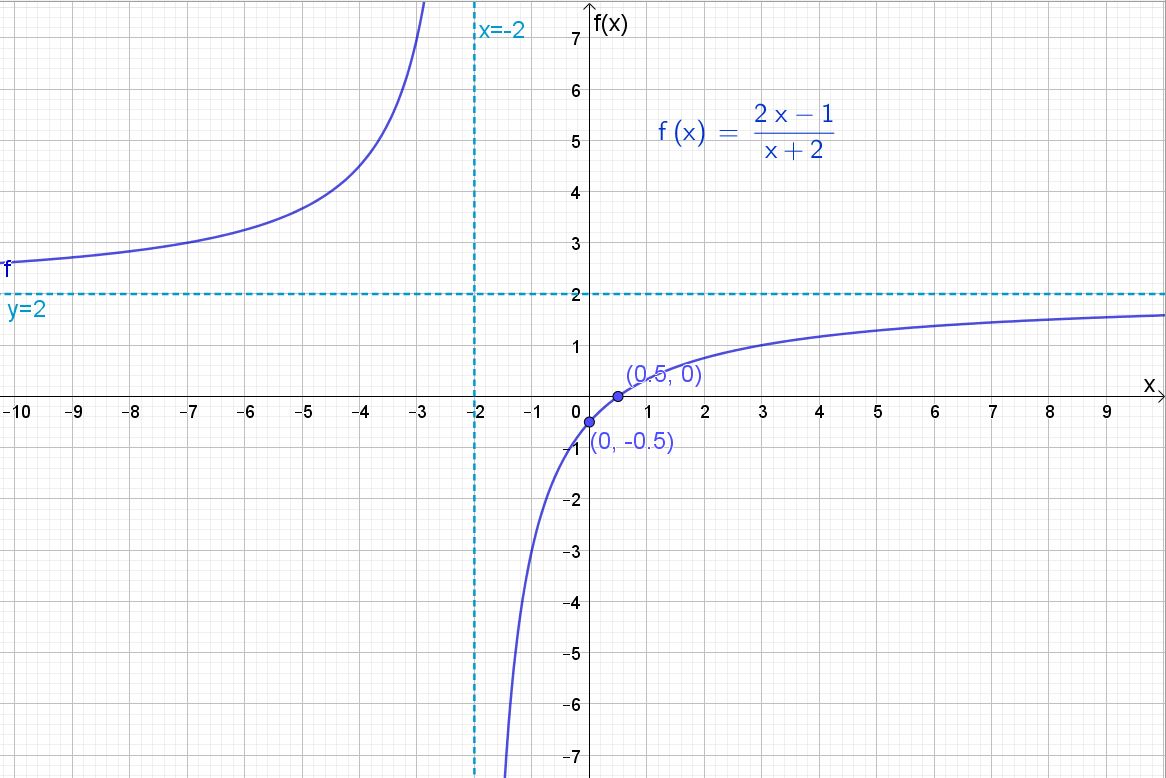
$f(x)=\frac{2x-1}{x+2} \quad , \quad x\neq -2$
Finner vertikal asymptote, som er den x-verdien som gir null i nevner, i dette tilfellet $x=-2$.
Finner horisontal asymptote ved å la x gå mot uendelig.
$$y=\lim_{x\to\infty} \frac{2x-1}{x+2} \approx \lim_{x\to\infty} \frac{2x}{x}=2$$
Finner nullpunktet (dvs. skjæringspunktet med x-aksen):
$\frac{2x-1}{x+2}=0 \quad | \cdot(x+2) \\ 2x-1=0 \\ x=\frac{1}{2}$
Finner skjæringspunktet med y-aksen, som er det samme som konstantleddet, i dette tilfellet $y= - \frac{1}{2}$
Skisserer grafen (du må gjøre det for hånd):
b)
Setter $f(x)=x-2$:
$\frac{2x-1}{x+2}=x-2 \quad | \cdot(x+2)$
$2x-1=(x-2)(x+2)$
$2x-1=x^2-2^2$ (konjugatsetningen)
$-x^2+2x+3=0 \\ x= \frac{-2 \pm \sqrt{2^2-4\cdot (-1) \cdot 3}}{2\cdot(-1)} \\ x= \frac{-2\pm \sqrt{4+12}}{-2} \\ x_1= \frac{-2+4}{-2} \quad \vee \quad x_2=\frac{-2-4}{-2} \\ x_1=-1 \quad \vee \quad x_2=3$
Oppgave 8
a)
$g(x)=2x^3+3x^2-12x$
$g'(x)=6x^2+6x-12$
b)
I topp- og bunnpunktet er $g'(x)=0$
$6x^2+6x-12=0 \quad |:6 \\ x^2+x-2=0 \\ x=\frac{-1 \pm \sqrt{1^2-4\cdot 1 \cdot (-2)}}{2\cdot 1} \\ x= \frac{-1\pm \sqrt{1+8}}{2} \\ x_1= \frac{-1-3}{2} \quad \vee \quad x_2=\frac{-1+3}{2} \\ x_1=-2 \quad \vee \quad x_2=1$
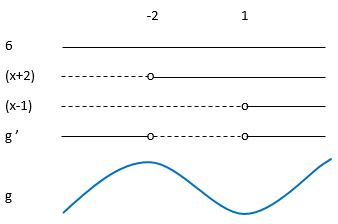
Faktoriserer $g'(x)=6x^2+6x-12=6(x+2)(x-1)$
Lager fortegnsskjema for $g'$ for å finne topp- og bunnpunkt på grafen til $g$.
$y_1=g(-2)=2\cdot(-2)^3+3\cdot(-2)^2-12\cdot(-2)=2\cdot(-8)+3\cdot 4 +24 = -16+12+24=20$
$y_2=g(1)=2\cdot 1^3+3\cdot 1^2-12\cdot 1=2+3-12 = -7$
Toppunktet på grafen til $g$ er $(-2, 20)$ og bunnpunktet er $(1,-7)$.
c)
Gjennomsnittlig vekstfart $a=\frac{y_2-y_1}{x_2-x_1}$
$x_1=0 \\ x_2=2 \\ y_1=g(0)=2\cdot0^3+3\cdot 0^2-12\cdot 0=0 \\ y_2=g(2)=2\cdot2^3+3\cdot 2^2-12\cdot 2=2\cdot8+3\cdot4-24=16+12-24=4$
$a=\frac{4-0}{2-0}=\frac{4}{2}=2$
Den gjennomsnittlige vekstfarten til $g$ i intervallet [0,2] er 2.
d)
$g'(x)=24 \\ 6x^2+6x-12 = 24 \\ 6x^2+6x-36=0 \quad |:6 \\ x^2+x-6=0\\ x=\frac{-1 \pm \sqrt{1^2-4\cdot 1 \cdot (-6)}}{2\cdot 1} \\ x= \frac{-1\pm \sqrt{1+24}}{2} \\ x_1= \frac{-1-5}{2} \quad \vee \quad x_2=\frac{-1+5}{2} \\ x_1=-3 \quad \vee \quad x_2=2 $
$y_1=g(-3)=2\cdot(-3)^3+3\cdot(-3)^2-12\cdot(-3)=2\cdot(-27)+3\cdot 9 +36 = -54+27+36=9$
$y_2=g(2)=4$ (fra oppgave c)
Den momentane vekstfarten er 24 i punktene $(-3,9)$ og $(2,4)$.
Oppgave 9
a)
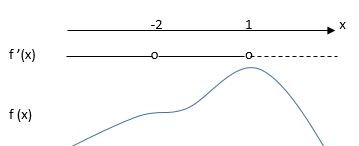
Grafen til $f$ stiger når $x<-2$ og $-2<x<1$. Grafen synker når $x>1$.
Du kan også skrive at grafen til $f$ stiger når $x\in \langle \leftarrow , 2 \rangle$ og $x\in \langle 2,1 \rangle$. Grafen synker når $x\in \langle 1, \rightarrow \rangle$.
Grafen til $f$ har et terrassepunkt i $x=-2$ og et toppunkt i $x=1$.
b)
DEL 2
Oppgave 1
Bruker CAS i Geogebra.
La x være prisen i kr per kilogram torsk, og y prisen i kr per kilogram sei.
Einar fikk 24,50 kr per kilogram torsk, og 20,50 kr per kilogram sei.
Oppgave 2
a)
For å bruke en binomisk sannsynlighetsmodell må vi ha at:
- Alle delforsøkene har to mulige utfall. Her at hver passager enten møter $(A)$, eller ikke møter $( \bar{A} )$ til flyavgang.
- Sannsynligheten for $A$ er den samme hele tiden. Her er $P(\bar{A})=0,06$ og dermed $P(A)=0,94$
- De enkelte delforsøkene er uavhengige av hverandre. I dette tilfellet må vi anta at hvorvidt en passager møter eller ikke møter til flyavgang, ikke påvirker sannsynligheten for om noen av de andre passagerene møter eller ikke møter. Vi må se bort fra tilfeller som at en hel familie lar være å møte dersom én i familien er syk, eller at flere passagerer ikke møter på grunn av én forsinket buss.
Kilde: ndla.no
b)
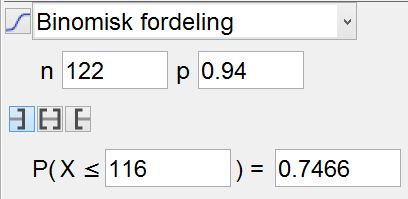
Bruker sannsynlighetskalkulatoren i Geogebra:
Sannsynligheten for at alle som møter får plass på flyet, er ca. 74,6%.
c)
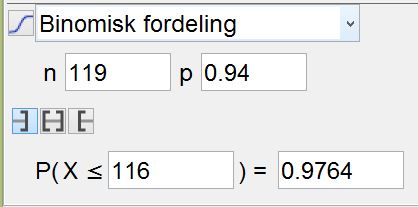
Prøver meg frem ved å endre på $n$ (totalt antall solgte billetter) i sannsynlighetskalkulatoren i Geogebra. Ser at dersom selskapet selger 119 billetter, er sannsynligheten for at alle som møter, får plass på flyet, ca. 97.6%.
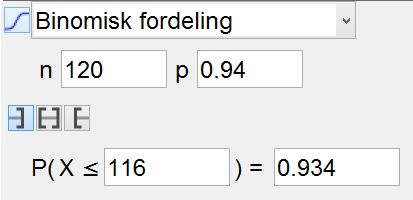
Dersom selskapet selger 120 billetter er sannsynligheten for at alle som møter, får plass på flyet, bare 93.4%.
Selskapet kan altså maksimalt selge 119 billetter.
Oppgave 3
a)
Frode og Peter produserer x kasser av type A og y kasser av type B. Vi har $x\geq 0$ og $y\geq 0$ fordi det må produseres null eller et positivt antall fuglekasser. Det er ikke mulig å produsere et negativt antall fuglekasser.
Fra oppgaveteksten vet vi at: Frode bruker 10 minutter på å lage delene til en kasse av type A og 30 minutter på å lage delene til en kasse av type B. I løpet av en uke kan Frode jobbe 15 timer. 15 timer er det samme som $15\cdot 60=900$ minutter. Dette gir oss ulikheten:
$10x+30y\leq 900 \quad |:10 \\ x+3y \leq 90 $
Fra oppgaveteksten vet vi at: Peter bruker 20 minutter på å sette sammen og male en kasse av type A og 30 minutter på en kasse av type B. I løpet av en uke kan Peter jobbe 20 timer. 20 timer er det samme som $20 \cdot 60=1200$ minutter. Dette gir oss ulikheten:
$20x+30y\leq 1200 \quad |:10 \\ 2x+3y \leq 120 $
b)
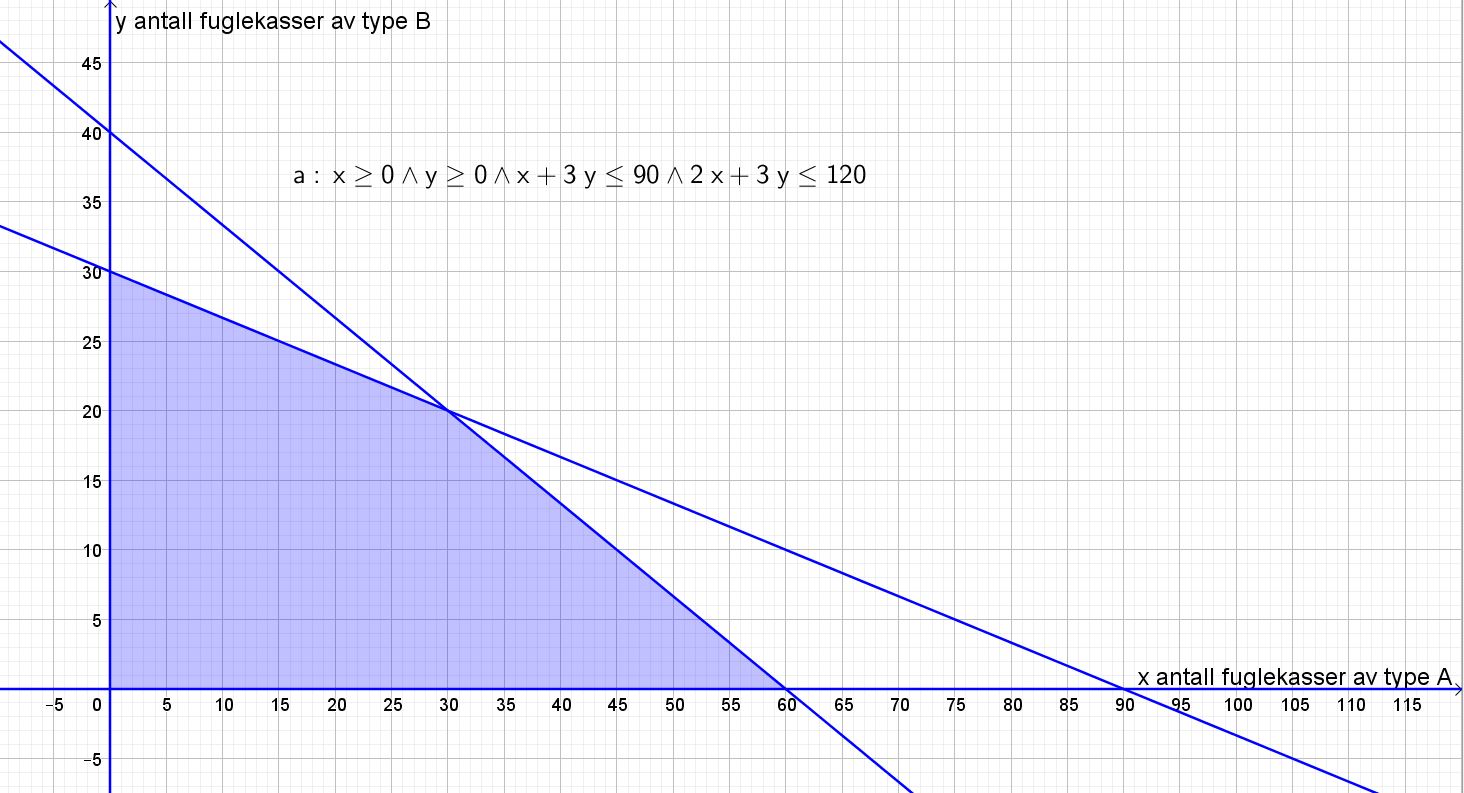
Bruker Geogebra.
c)
Likningen for fortjenesten blir $I=60x+150y$.
Tegner inn linjene $x=0,\,y=0,\,x+3y=90,\,2x+3y=120$ i Geogebra. Lager glider for fortjenesten ved å skrive $60x+150y=I$ (NB: du må skrive =I til slutt for at Geogebra skal foreslå å lage glider).
Finner at den største fortjenesten får vi i punktet $A=(30,20)$. Det vil si at Frode og Peter bør produsere 30 kasser av type A, og 20 kasser av type B for at fortjenesten skal bli størst mulig.