Løsning del 2 utrinn Vår 13

Oppgave 1

480kr + 145kr + 95kr<Math>\cdot</Math>4 + 950 kr = 1955kr

Hun betaler 25%: 1955kr <Math>\cdot</Math> 0,25 = 489kr.

Oppgave 2

a)

Hun kan velge på <Math>11 \cdot 10 \cdot 8 = 880</Math> måter.

b)

Sannsynligheten for at hun både velger riktig børste og riktig tråd er <Math> \frac{1}{11} \cdot \frac{1}{8} = \frac{1}{88}</Math>

Oppgave 3

Blandet i forholdet 1:3 gir det 1200ml ferdig blanding. Hun bruker 80ml daglig.

1200 : 80 = 15, dvs. en flaske varer i femten dager.

Oppgave 4

<Math>V= \frac{\pi \cdot h}{3} (R^2 + r \cdot R + r^2) = \frac{8\pi}{3} (3,3^2+2,3 \cdot 3,3 + 2,3^2) cm^3 = 199,1 cm^3 \approx 2dl</Math>

Oppgave 5

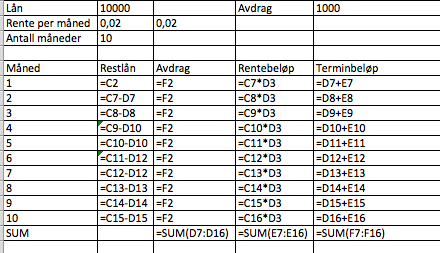
a)

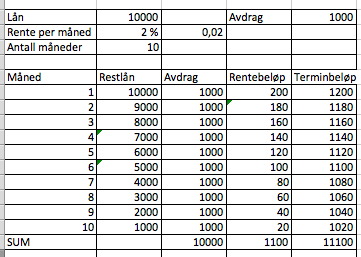
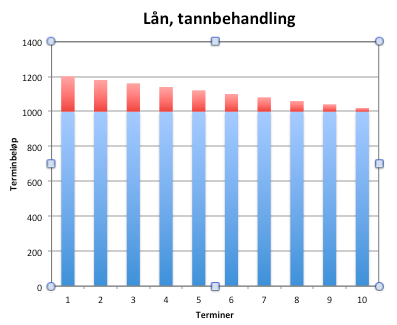
b)

Rødt markerer rente og blått avdrag.

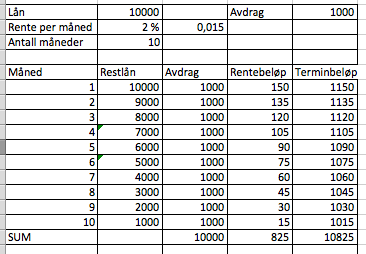
c)

Hun kan spare 1100 kr - 825kr = 275 kr ved å velge dette lånet.

Oppgave 6

a)

<Math>h(x) = -0,05x^2+x+2 \\ h(10) = -0,05 \cdot 100 + 10 + 2 = -5 +10 + 2 =7</Math> ,

dvs. syv meter over bakken etter ti meter fra Rampe 1.

b)

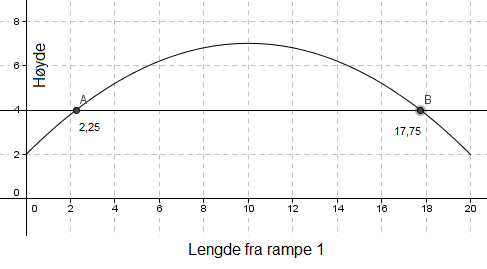
Brukte kommandoen Funksjon[<Funksjon>,<Start>,<Slutt>] for å tegne grafen for x-verdier mellom 0 og 20.

c)

Motorsykkelen er 4 meter over bakken to steder, etter 2,25 meter på vei opp, og etter 17,75 meter på vei ned, målt fra Rampe 1. Se bilde i b).

Oppgave 7

a)

Trekant AOC er likebeint der siden AO = OC = 5,0 cm, fordi vinkel A og C begge er 45 grader, kan også se at OC = 5,0 cm ved å legge merke til at den er radien i sirkelen. Trekanten er rettvinklet og man kan bruke Pytagoras:

<Math>(AC)^2 = (5cm)^2 + (5cm)^2 \\ AC = \sqrt{50} cm</Math>

b)

Arealet til halvsirkelen ABC: <Math>A = \frac{\pi r^2}{2} = \frac{25\pi cm^2}{2} = 12,5 \pi cm^2 =39,25 cm^2</Math>

Oppgave 8

Lengden av den blå linjen:

<Math>O = AEC_{sirk} + CB_{sirk} + BH + HG + GA \\ O = 2 \pi \frac{\sqrt{50}}{4} cm + \frac{2 \pi \cdot 5}{4} cm +10cm +10cm +10cm \\ O = ( \frac{\sqrt{50}\pi}2 + \frac 52 \pi +30)cm \\ O = 48,96 cm</Math>

Oppgave 9

Areal av halvsirkelen ACEA: $A_{ACEA} = \frac 12 \pi \cdot (\frac{\sqrt {50}}{2})^2 = \pi \frac{50}{8}$

Arealet av halvsirkelen ABCA: $A_{ABCA} = \frac 12 \pi \cdot 25 = \pi \frac{25}{2}$

$ \frac{A_{ACEA}}{A_{ABCA}} = \frac{ \pi \frac {50}{8}}{\pi \frac{25}{2}} = \frac 12 $

Ved inspeksjon ser man at kvadratet AFBC er halvparten av AGHB, fordi trekanten ABC kan flyttes til HBF. Det lille kvadratet dekker da halvparten av det store. Diagonalen AH.

Ver regning finner man at arealet av AGHB er 100. Sidekantene i AFBC er$\sqrt{50}$, så arealet er 50, dvs forholdet mellom arealet av det lille og det store kvadratet er $\frac{50}{100} = \frac 12$, altså det samme som mellom halvsirklene over.

Oppgave 10

<Math>(AC)^2 = r^2+r^2 \\ (AC)^2 = 2r^2 \\ AC = \sqrt2r </Math>

AD er radius i halvsirkelen AEC : AD = r' = <Math>\frac12 \sqrt2r</Math>

Areal av trekanten AOC : <Math>A = \frac{Gh}{2} = \frac{r \cdot r}{2} = \frac{r^2}2</Math>

Areal av halvsirkelen AEC: <math>A = \frac{\pi (\frac{\sqrt2r}{2})^2}{2} = \frac{\pi r^2}{4}</math>

Areal av kvartsirkelen AOC: <math> A= \frac{\pi r^2}{4}</math>

Arealet av halvmånen blir : A = halvsirkel AEC - ( kvartsirkel AOC - trekant AOC)

<math> A = \frac{\pi r^2}{4} - \frac{\pi r^2}{4} + \frac{r^2}2 = \frac{r^2}2 </math>