R1 2015 vår LØSNING
Diskusjon av denne oppgaven på matteprat
Løsningsforslag (pdf) fra bruker joes. Send gjerne en melding hvis du oppdager feil i fasit. På forhånd, takk.
DEL EN
Oppgave 1
a)
b)
c)
Oppgave 2
a)
Altså er polynomet delelig med x - 2.
b)
Løser
P(x) = ( x - 2)( x + 1)(x + 3)
c)
Oppgave 3
Oppgave 4
Sirkelen har radius 5, med sentrum i punktet (1, -2).
Oppgave 5
Oppgave 6
Oppgave 7
Oppgave 8
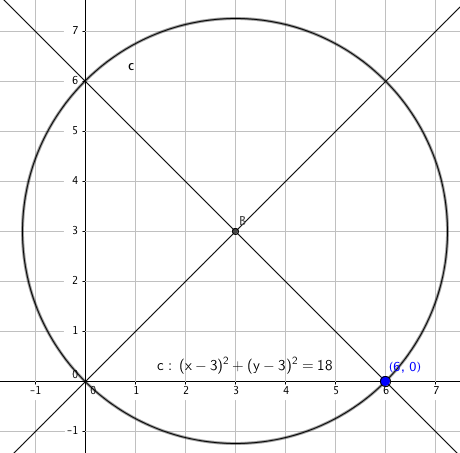
a)
Vinkel B er en pereferivinkel som spenner over buen AC. Vinkel CSA er en sentralvinkel som spenner over sammen buen. Vinkel DSA er halvparten av vinkel CSA. Vinkel B er derfor lik vinkel DSA.
b)
c)
Oppgave 9
Setter
Må forkaste u= -3 og får
DEL TO
Oppgave 1
a)
b)
Fra tegningen i a ser man at likningen blir
Oppgave 2
a)
b)
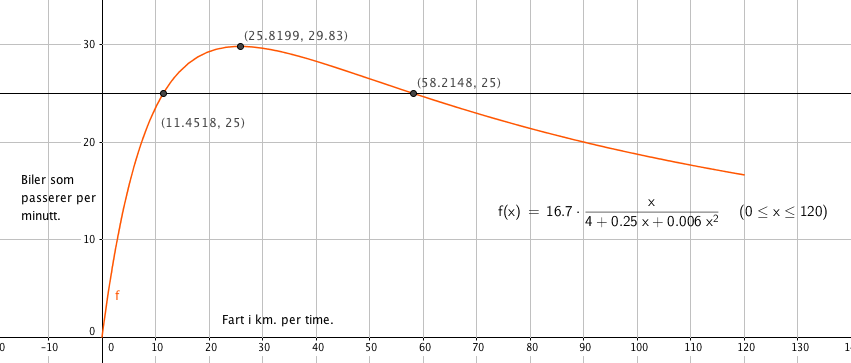
Fra Figuren i a leser vi at farten må være 12 - 58 km/h.
c)
Det passerer flest biler, ca. 30 stykker per minutt, når farten er ca. 26 km/h.
Oppgave 3
Oppgave 4
a)
b)
Oppgave 5
a)
Vi har nå funnet stigningstallet til tangenten i P. Finner så b i likningen for den rette linje:
Innsatt i y= ax + b gir det: