S1 2015 vår LØSNING
Diskusjon av denne oppgaven på matteprat
Løsning laget av matteprat-bruker LektorH
DEL EN
Oppgave 1
a)
$2x^2-6x+4=0 \\ x= \frac{6 \pm \sqrt{36 -4 \cdot 2 \cdot 4}}{2 \cdot 2} \\ x= \frac{6 \pm 2}{4} \\ x=1 \vee x= 2$
b)
$2lgx - lg2 = lg(4-x) \\ lg{ \frac{x^2}{2}} = lg(4-x) \\ 10^{ lg{ \frac{x^2}{2}}} = 10^{lg(4-x)} \\ \frac{x^2}{2} = 4-x \\ x^2+2x-8=0 \\ x= \frac{-2 \pm \sqrt{4-4 \cdot 1 \cdot (-8)}}{2} \\ x= \frac{-2 \pm 6}{2} \\ x= -4 \vee x =2$
Likningen inneholder lgx, så alle negative løsninger må forkastes.
Dvs. x = 2. Ved å sette prøve på svaret ser man at begge sider gir lg2.
Oppgave 2
a)
$PC + CB = 30 = x + y$ Det er like langt fra B til P, om C og om A, derav første likning.
$(10+x)^2+400 = y^2$ er Pytagoras anvendt på trekanten ABC.
b)
<math> \left[ \begin{align*} x+y=30\\ (10+x)^2+400 = y^2 \end{align*}\right] </math>
<math> \left[ \begin{align*} x=30 - y \\ (10+30-y)^2+400 = y^2 \end{align*}\right] </math>
<math> \left[ \begin{align*} x=30 - y \\ (1600 -80y +y^2 +400 = y^2 \end{align*}\right] </math>
Den nederste likningen gir: 80y = 2000, dvs. y = 25
$x = 5 \vee y = 25$
Oppgave 3
a)
$(a+1)^2 - 2(a-1)(a+1) + (a-1)^2 = \\ a^2+2a+1 -2(a^2-1) +a^2 -2a+1=\\ a^2 +2a+1-2a^2+2+a^2-2a+1=\\ 4$
b)
$\frac{(2a^2)^{-1}(3b)^2}{(3a^2b^{-1})^2} \\ \frac{9b^2b^2}{18a^6}= \\ \frac{b^4}{2a^6}$
Oppgave 4
a)
$f(x)= x^3 -6x^2+9x-4 \quad D_f = \R \\ f´(x) = 3x^2-12x+9$
b)
Setter den deriverte lik null for å finne ekstremalpunkter:
$f´(x) = 0\\ 3x^2-12x+9 =0 \\x = \frac{4 \pm \sqrt{16-12}}{2} \\ x=1 \vee x= 3 $
Faktorisert:
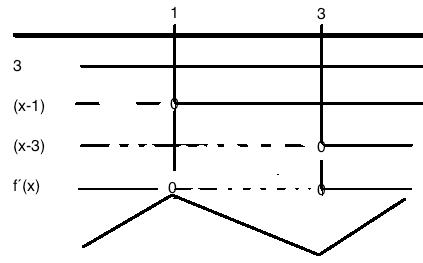
$f´(x)= 3(x-1)(x-3)$
$f´(2) = $ negativ verdi, så:
Maksimumspunkt: $f(1)= 1-6+9-4 = 0$. dvs. (1,0).
Minimumspunkt: $f(3)= 27-54+27-4 =-4$. dvs. (3, -4).
c)
Likning til tangenten til grafen i (0, f(0)):
f(0) = -4
f´(0) = 9
$ y= ax+b \\ y= 9x+b \\ -4 = 9 \cdot 0 +b \\ b=-4 \\ y= 9x-4$
d)
Den deriverte til den andre tangenten må være 9.
$f´(x)=9 \\ x= 0 \vee x =4$
f(4)=0
Den andre tangenten med stigningstall 9 tangerer i punktet (4,0)
Oppgave 5
a)
b)
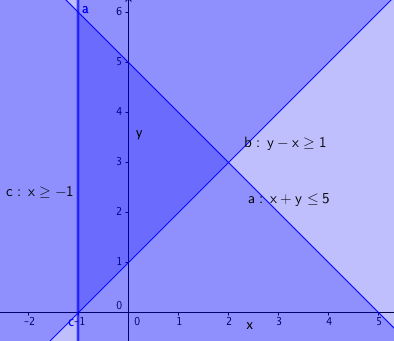
Sjekker hjørnene i trekanten (-1, 0), -1, 6) og (2, 3)
$3x+2y \\ 3 \cdot (-1) +0 = -3 \\ 3 \cdot (-1) + 2 \cdot 6= 9 \\ 3 \cdot 2 + 2 \cdot 3 = 12$
Uttrykket blir størst i punktet (2, 3)
Oppgave 6
a)
$K(x)= 0,25x^2+100x + 5000 \quad x \in [0, 400]$
Inntekt er : $I(x) = 200x$
Overskudd = Inntekt - Kostnad:
$O(x)= I(x)-K(x) \\ O(x)= 200x- 0,25x^2-100x-5000 \\ O(x)= -0,25x^2 + 100x - 5000$
b)
$O´(x) = -0,5x+100$
Setter den deriverte lik null og får løsningen x = 200.
200 solgte enheter gir størst overskudd.
Oppgave 7
a)
Sannsynlighet for to røde kuler:
$ P(2 røde)= \frac{ \binom{3}{2} \binom{4}{1}}{ \binom{7}{3}} = \frac{\frac{3!}{2! \cdot 1!} \cdot \frac{4!}{1! \cdot 3!}}{ \frac{7!}{3! \cdot 4!}} = \frac{3 \cdot 4}{35}= \frac{12}{35}$
b)
Flere røde enn blå:
p( flere røde enn blå) = P(2 røde) + P (3 røde)= $\frac{12}{35} + \frac{\binom{4}{0} \binom{3}{3}}{ \binom{7}{3}} = \frac{12}{35} + \frac{1}{35} = \frac{13}{35}$
c)
Med tilbakelegging har vi en binomisk situasjon der p= $\frac 37$, n = 3 og x = 2 :
P(2 røde) = $ \binom{3}{2} \cdot ( \frac 37)^2 \cdot ( \frac 47) = \frac{108}{343} $
Det er ca en tredjedels sjanse for at to av kulene er røde.
Oppgave 8
a)
Graf A kommer fra en brøkfunksjon, altså h eller g. Begge har vertikal asymptote for x = 1, så det hjelper oss ikke. Dersom vi deler alle ledd i teller og nevner på x vil vi lett se den horisontale asymptoten, når vi lar x gå mot uendelig. h har vertikalasymptote for y = 2 og g har for y =1. Det er altså h som er fremstilt i graf A.
b)
Graf B har en form som tilsier at det kan være en tredjegradsfunksjon. Da har vi kandidatene f og k. Både f og k skjærer y-aksen i 2, så det hjelper oss ikke. Vi sjekker den deriverte for x=0.
$f´(x)=3x^2+2x-2,\quad f´(0) = -2 \\ k´(x)=6x^2-6. \quad k´(0)= -6$
Begge de deriverte er negative, så det er vanskelig å konkludere. Sjekker ekstremalpunkt for $x= \pm 1$:
$f´(1) =3 \\ k´(1)= 0 \wedge k´(-1)=0$
Vi ser at f ikke passer pga minimum i x=1, men k(x) er funksjonen til graf B.
Oppgave 9
$9^x-3^x-12=0 \\ (3^2)^x -3^x-12 =0 \\ 3^{2x}-3^x-12 =0 \\(3^x)^2 -3^x-12=0 \\ u= 3^x \\ u^2-u-12 =0 \\ u = \frac{1 \pm{\sqrt{1+48}}}{2} \\ u = -3 \vee u = 4 \\ $
$3^x$ kan ikke være negativ, så kun 4 er en løsning for u.
$3^x=4 \\ 3^x =2^2 \\ x \lg3 = 2 \lg2 \\ x= \frac{2 \lg2}{\lg3}$
DEL TO
Oppgave 1
a)
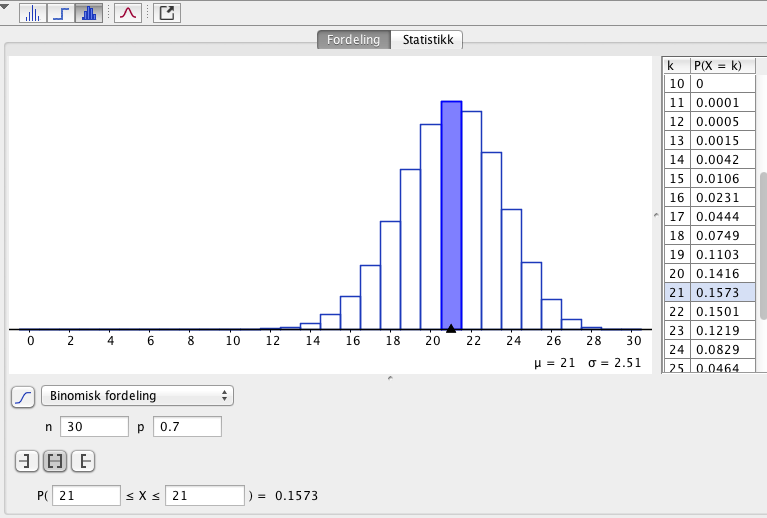
Vi antarat de er fornøyde uavhengig av hverandre, og at populasjonene er mye større enn utvalget. Bruker binomisk fordeling
Det er ca. 15,7% sannsynlig at 21 elever blir fornøyde.
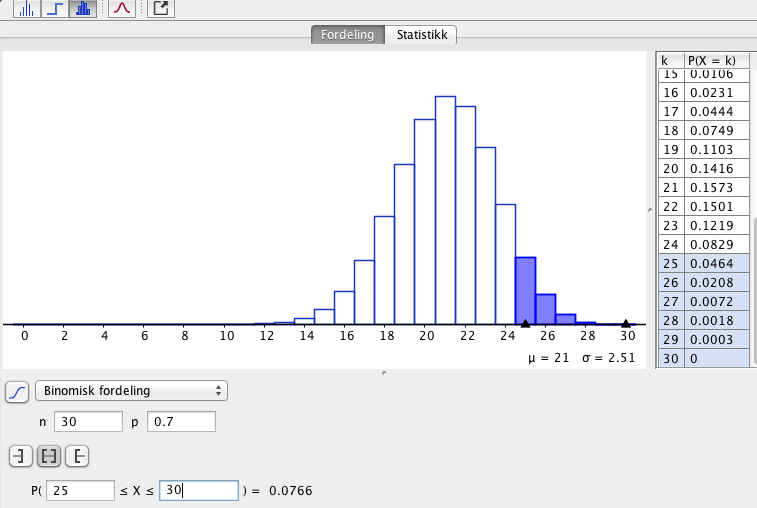
b)
Det er ca. 7,7% sannsynlig at minst 25 av elevene blir fornøyde.
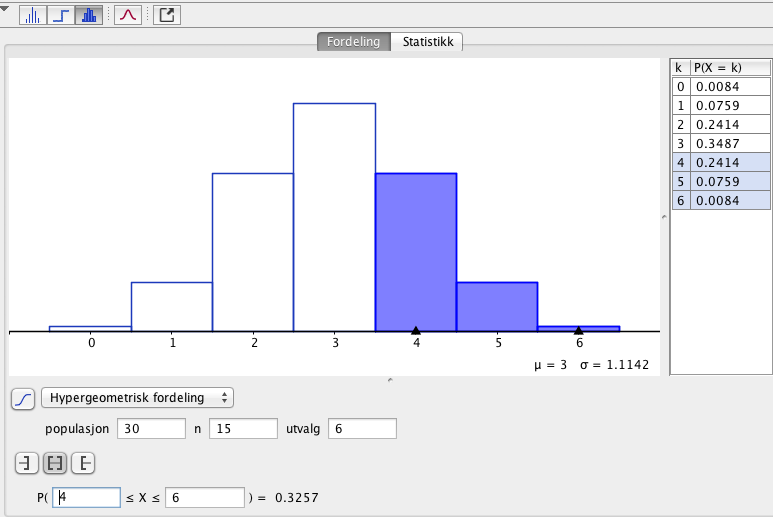
c)
Det er 32,6% sannsynlig at det trekkes flere jenter enn gutter.
Oppgave 2
a)
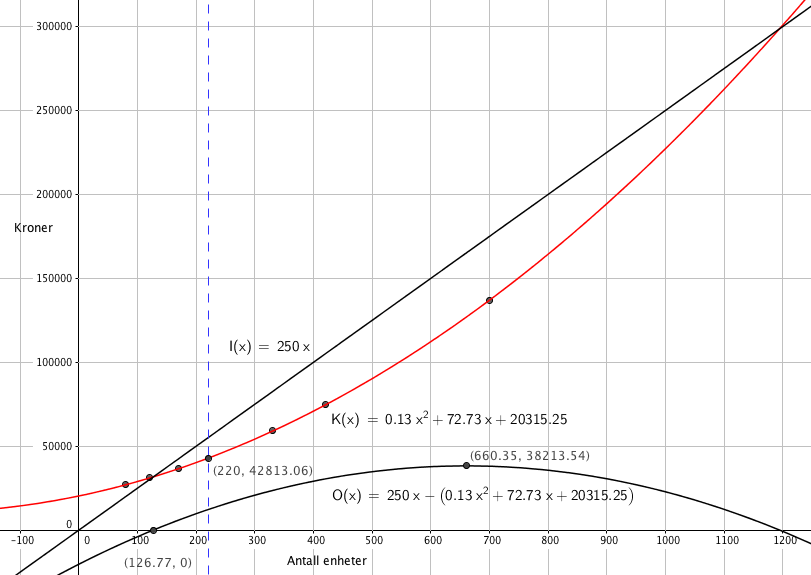
En god modell er $K(x)=0,13x^2+72,73x+20315$
Kostnadene ved å produsere 220 enheter er 48.813 kroner.
b)
Fra figur i a:
For å få overskudd må bedriften produsere og selge mellom 127 og 1194 enheter.
c)
Fra figur i a:
Størst overskudd ved 660 enheter, da er overskuddet 38.213,50 kr.
Oppgave 3
a)
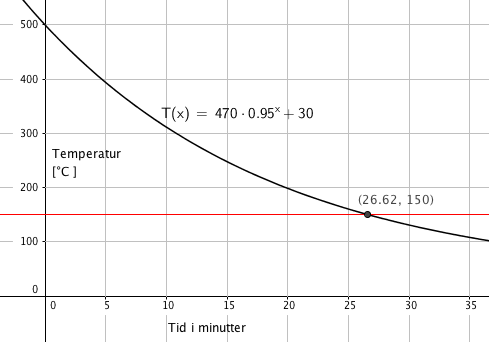
Metallet er 500 grader celsius når det blir tatt ut av ovnen, fra figur. Har også at $T(0)= 470+30 = 500$
b)
Smeden har ca 26,5 minutter til å bearbeide metallstykket. Det er varmt i rommet, 30 grader celsius ( konstanledd i funksjonsuttrykk).
c)
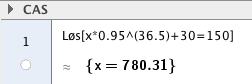
Finner ønsket temperatur ved å løse:
$T_s 0,95^{36,5} = 150$
Bruker CAS:
Temperaturen på arbeidsstykket må være ca: 780 + 30 = 810 grader.
Oppgave 4
a)
Areal av eskens bunn: $A= (6-4x)(6-2x) = \\36-12x-24x+8x^2= \\ 8x^2-36x+36 $
Multipliserer så med høyden av esken, x, og får volumet:
$V(x) = A(x) \cdot x= 8x^3-36x^2+36x \quad x \in <0, 1,5>$
b)
Deriverer V ved hjelp av CAS. finner nullpunkt. Størst volum får man når x er 0,63 dm, 6,3 cm. Da er volumet ca. $10,4 dm^3$, eller 10,4 liter.
c)
Både a og x er positive verdier i denne praktiske oppgaven. Vi ser at linje 5 gir oss det maksimale volumet vi ble bedt om å vise.