1T 2015 høst LØSNING

• Diskusjon av denne oppgaven på matteprat

• Løsning del 1 postet på matteprat av LektorH

• Løsning del 2 postet på matteprat av LektorH

DEL EN

Oppgave 1

$1,8 \cdot 10^{12} \cdot 0,0005 = \\ 1,8 \cdot 10^{12} \cdot 5 \cdot 10^{-4} = \\ 1,8 \cdot 5 \cdot 10^{12-4} = \\ 9,0 \cdot 10^{8}$

Oppgave 2

<math> \left[ \begin{align*}2x+3y = 13 \\ 4x-2y=2 \end{align*}\right] </math>

Ganger første likning med -2:

<math> \left[ \begin{align*}-4x-6y = -26 \\ 4x-2y=2 \end{align*}\right] </math>

Legger sammen likningnene og x forsvinner:

<math> \left[ \begin{align*}-8y= -24 \end{align*}\right] </math>

Det gir y = 3. Innsatt i en av likningnen gir det x = 2. Løsning er altså $x=2 \wedge y=3$

Oppgave 3

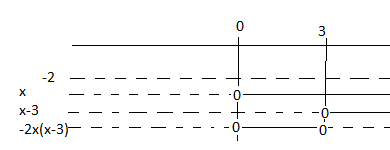
$-2x^2+6x<0 \\ -2x(x- 3)<0$

Fortegnsskjema:

$x \in < \leftarrow, 0> \cup < 3, \rightarrow>$

Oppgave 4

$( \sqrt 2 )^2+ \frac {\sqrt8}{2} +\sqrt[3]{8} - \frac{\sqrt[3]{128}}{\sqrt[3]{2}}= \\ 2 - \sqrt 2 + 2 - \frac{\sqrt[3]{2^7}}{\sqrt[3]{2}} = \\2 - \sqrt 2 + 2 - \frac{4\sqrt[3]{2}}{\sqrt[3]{2}} = \\ -\sqrt 2 $

Oppgave 5

$x^2+bx +c=0$ Løsninger $x_1= -4 \wedge x_2=2$

Setter inn for x:

$16-4b+c=0 \wedge 4+2b+c=0$

Multipliserer den siste med -1 og legger dem sammen:

12- 6b = 0 gir b = 2. Ved innsetting finner man c = -8

$x^2+2x - 8=0$

Oppgave 6

$\frac{x+1}{x-1} - \frac{x-3}{2x-2} + \frac 12 =\\ \frac{2x+2-x+3+x-1}{2(x-1)}=\\ \frac{2x+4}{2(x-1)} = \\ \frac{x+2}{x-1} $

Oppgave 7

$\frac{x^2-4xy+4y^2}{3xy- 6y^2} = \\\frac{(x-2y)^2}{3y(x-2y)} = \\ \frac{x-2y}{3y}$

Oppgave 8

$2^{4x} \cdot 2^{x^2} = 32 \\ 2^{x^2+4x} = 2^5 \\ x^2+4x-5=0 \\ x= \frac{-4 \pm \sqrt{16+20}}{2} = \\ x= -5 \vee x = 1$

Oppgave 9

Katetene er like lange. Lengde x:

$x^2 + x^2 = ( \sqrt2)^2 \\ 2x^2=2 \\ x =1$

Arealet blir da halvparten av en ganger en. A = 0,5

a)

$f(x)= x^2-x-2$

$f(x)=0 \\ x^2-x-2 =0 \\ x= \frac{1 \pm \sqrt{1+8}}{2} \\ x= -1 \vee x = 2$

Nullpunkter er (-1,0) og (2, 0)

b)

Koefisienten foran andregradsleddet er positiv, det betyr at grafen vender sin hule side opp, og har et minimumspunkt. Dette ligger på symmetrilinja som er x= 0,5.

$f(0,5) =$

Eller vi kan derivere og sette den deriverte lik null:

$f'(x): 2x+1 \\f'(x)=0 \\ x = - \frac 12$

Oppgave 11

Formlikhet.

Dersom k er gjennomsnittet av lengdene til det parallelle sidene i det lille trapeset, er tilsvarende lengde i det store trapeset 3k.

Arealet av det lille trapeset er kh = A

Arealet av det store trapeset er $3k\cdot 3h = 9kh = 9A$