R1 2013 vår LØSNING
Løsningsforslag som pdf laget av claes
DEL EN
Oppgave 1
Oppgave 2
a)
b)
Oppgave 3
a)
b)
c)
Oppgave 4
Oppgave 5
f er kontinuerlig for
f er deriverbar for
Oppgave 6
vendepunkt;
Vendetangent;
Stigningstall:
Tangent:
Oppgave 7
a)
Dersom
b)
Oppgave 8
a)
b)
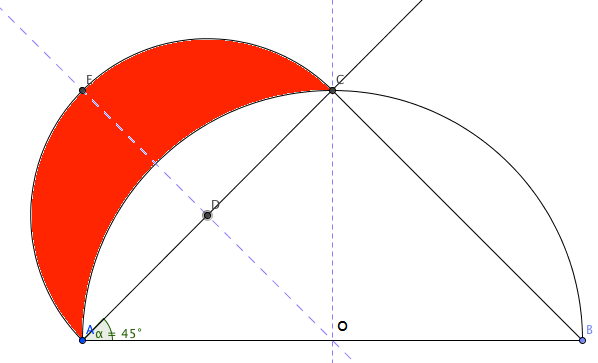
Kvartsirkel AOD:
Sirkelsegment ADC:
Halvsirkel AEC:
Hippokratesmånen ( den røde flaten):
Vi ser at de to arealene er like store.
DEL TO
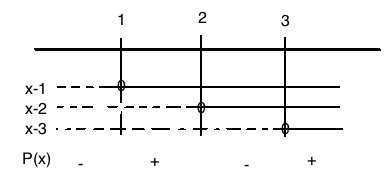
Oppgave 1
a)
Grafen til f skjærer x-aksen i x = -1 og er derfor delelig med (x+1), videre skjærer den i x = 1 og er derfor delelig med (-1). Den skjærer også i x = 3 og er derfor delelig med (x-3). En tredjegradsfunksjon kan maksimalt ha tre nullpunkter. Det har denne.
Konstanten a bestemmer "utslaget" til maksimums og minimumspunktene
b)
c)
Vi vet fra før at x = 0 er en løsning. Vi skal finne den andre og setter opp likningen:
Her kan vi dele på 4 på begge sider. Vi kan også dele på (x-3) dersom x = 3 ikke er en løsning av likningen. Dersom x=3 deler vi på null, og det gir ikke menming. Vi tester om x=3 er en løsning, og finner at det er tilfelle. Det andre skjæringspunktet blir derfor (3, 0).
Oppgave 2
a)
b)
Parameterfremstilling for linjen gjennom A og
Punkt A (1,1) og rettningsvektor [3, 2] gir:
Parameterfremmstilling for linjen gjennom C og
Punktet C (3, 4) og rettningsvektor
c)
Søker skjæringen mellom de to linjene i oppgave b og får:
Dvs, T har koordinatene
Oppgave 3
a)
Skjæring med y akse, x = 0 :
Skjæring med x akse, y = 0:
Forkaster t = 0 og får
b)
c)
Oppgave 4
a)
Pytagoras:
Areal av rektangel :
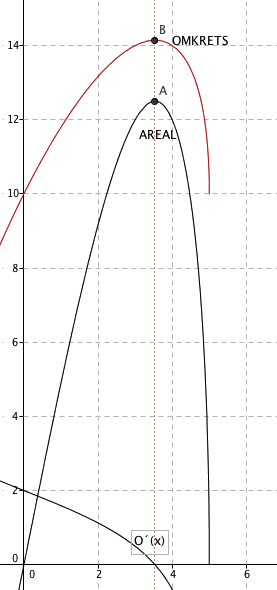
b)
Fra Geogebra ser man at arealet er størst når x = 3,54. Da er
c)
Omkrets er to x pluss to y:
Man observerer at O´(x) = 0 når x = 3,54. Altså er omkretsen også størst når figuren er et kvadrat.
Oppgave 5
6 røde kuler, 4 svarte kuler, totalt 10 kuler.
Trekker to kuler.
Definerer hendelser
A: to kuler med ulik farge
B: to kuler med lik farge.
a)
b)
c)
Oppgave 6
Likningen har en løsning når grunntallene på begge sider er lik en, dvs. x = n er en løsning.
Det er også
Altså blir løsningen: