2P 2011 vår LØSNING
MAT 1015
Del 1
Oppgave 1
a)
1) <math> 36 200 = 3.62 \cdot 10^4 </math>
2) <math> 0.000 642 = 6.42 \cdot 10^{-4} </math>
3) <math> 53 \text{ millioner} = 5.3 \cdot 10^7 </math>
4) <math> 0.034 \cdot 10^{-2} = 3.4 \cdot 10^{-4} </math>
b)
| Prosentvis endring | Vekstfaktor |
| + 2% | 1 + 0,02 = 1,02 |
| - 68 % | 1-0,68 = 0,32 |
| -75% | 0,25 |
| + 100% | 2 |
c)
1) <math>a^4 \cdot \big( a^2 \big)^{-3} \cdot a^0 = a^4 \cdot a^{2 \cdot (-3)} \cdot a^0 = a^4 \cdot a^{-6} \cdot a^0 = a^{4 - 6 + 0} = a^{-2}</math>
2) <math>\frac{2^{-3} \cdot 4^3 } {8^2} = \frac{2^{-3} \cdot (2^2)^3 } {(2^3)^2} = \frac{2^{-3} \cdot 2^6 } {2^6} = 2^{-3} = \frac{1}{8} </math>
d)
0, 0, 2, 2, 2, 3, 4, 5, 5, 5
1)
Median = <Math>\frac {2+3}{2} = 2,5</Math>
Gjennomsnitt = <Math>\frac {2+2+2+3+4+5+5+5}{10} = 2,8</Math>
2)
| Antall Mål | Frekvens | Kumulativ Frekvens |
| 0 | 2 | 2 |
| 1 | 0 | 2 |
| 2 | 3 | 5 |
| 3 | 1 | 6 |
| 4 | 1 | 7 |
| 5 | 3 | 10 |
3) Den kumulative frekvensen for to mål er fem. Det betyr at i fem av kampene ble det skåret to mål eller mindre.
e)
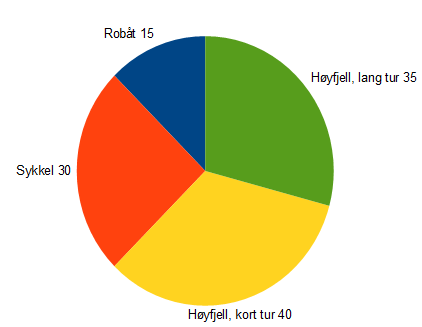
| TUR | Antall elever | Gradetall, sektor |
| Robåt | 15 | $ \frac{15 \cdot 360^{\circ}}{120} = 45^{\circ}$ |
| Sykkel | 30 | $ \frac{30 \cdot 360^{\circ}}{120} = 90^{\circ}$ |
| Høyfjell, kort løype | 40 | $ \frac{40 \cdot 360^{\circ}}{120} = 120^{\circ}$ |
| Høyfjell, lang løype | 35 | $ \frac{35 \cdot 360^{\circ}}{120} = 105^{\circ}$ |
f)
Grunnlaget er forskjellig. I begge butikkene er prisen 100%. I den ene øker prisen med 20%, da blir den nye prisen 120%. I den andre butikken øker prisen med 10%, da blir den nye prisen 110%. Så øker den med 10% igjen, denne gangen av 110% som gir en total på 11% av det som var før første økning, dvs. en økning på 121%
En vare som koster 100 kroner og blir satt opp 20% koster da 120 kroner.
En vare som koster 100 kroner og blir satt opp 10% koster da 110 kroner. Når den blir satt opp nye 10% er det med grunnlag 110 kroner. 10% av 110 kr. er 11 kroner. Ny pris blir da 121 kroner.
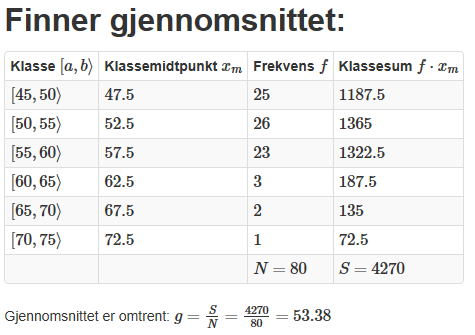
g)
| Antall minutter | Midtpunkt, $x_m$ | Antall elever, f | $x_m \cdot f$ |
| [0,30> | 15 | 1 | 15 |
| [30,60> | 45 | 3 | 135 |
| [60,120> | 90 | 5 | 450 |
| [120, 240> | 180 | 1 | 180 |
| SUM | 10 | 780 |
Vi forutsetter at elevene i de forskjellige intervallene fordeler seg jevnt rundt midtpunktet i intervallet. Dette er derfor en for tilnærming.
Gjennomsnitt $\frac{780}{10} = 78$ minutter.
h)
I tillegg til titallsystemet som vi er relativt godt kjent med har vi blant annet totall- og firetallsystemet.
Totallsystem: 64 - 32 - 16 - 8 - 4 - 2 - 1
Firetallsystem: 16 - 4 - 1
$27_{10} = 16 + 8 + 2 + 1 = 1 \cdot 2^4 + 1 \cdot 2^3 + 0 \cdot 2^2 + 1 \cdot 2^1 + 1 \cdot 2^0 = 11011_2 $
I følge tabellen i oppgaven skal det tilsvare 123 i firetallsystemet. Det betyr at vi trenger en av sekstengruppen to firere og tre enere:
$ 27_{10} = 1 \cdot 16_{10} + 2 \cdot 4_{10} + 3 \cdot 1_{10} = 123_{4} $
Første rad blir da:
$27_{10} =11011_2 =123_{4}$
$ 101010_2 = 1 \cdot 2^5 + 0 \cdot 2^4 + 1 \cdot 2^3 +0 \cdot 2^2 + 1 \cdot 2^1 + 0 \cdot 2^0 = 32 + 0 +8 + 0+ 2 + 0 = 42_{10}$
Fra firetallsystemet over ser man at det trengs to sekstengrupper, to firergrupper og to energrupper, det blir 32 + 8 + 2, i firetallsysemet: $ 222_4$
Tabellen blir da:
$27_{10} =11011_2 =123_{4}$
$42_{10} = 101010_2= 222_4$
Oppgave 2
a)
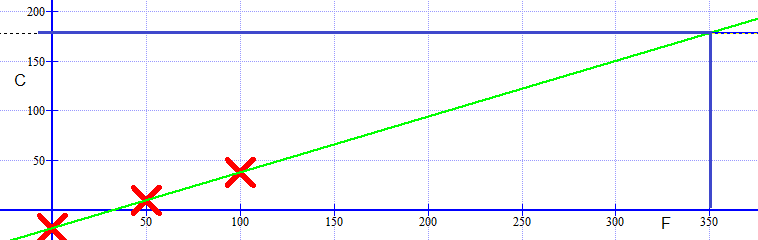
| $^\circ$F | 0 | 50 | 100 |
| $^\circ$C | -18 | 10 | 38 |
b og c)
Kaka skal stekes på $178^\circ C$
Del 2
Oppgave 3
a)
1)
2)
b)
1)
2)
c)
Oppgave 4
a)
b)
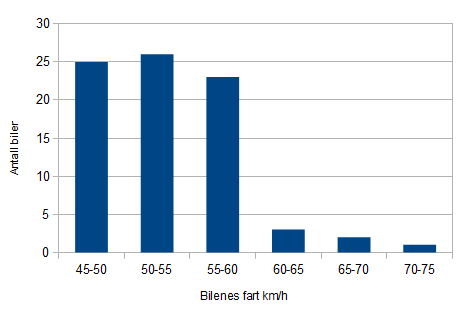
50 sone: ti prosent for fort, eller mer vil si alle biler som kjører i 55 km/h eller fortere.
Det er totalt 29 biler som kjører for fort, av 80. : $\frac{29}{80} \cdot 100 \percent = 36,3 \percent $
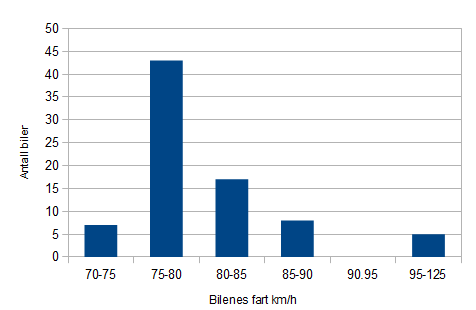
80 sone: ti prosent for fort, eller mer vil si alle biler som kjører 88km/h eller fortere. Åtte biler kjører mellom 85 og 90 km/h. Dersom man antar at bilene fordeler seg jevnt i intervallet, (noe vi ikke har holdepunkter for ut fra dataene), vil ca. tre biler ligge over 88 km/h. Det vil da til sammen være 8 biler som kjørere mer enn 10% for fort, av 80 biler. Det er 10% av de bilene som ble målt.
c)
FEMTISONE:
ÅTTISONE:
d)
Her testes prosentvis del av det hele nok en gang, litt fantasiløst og unødvendig, men her er løsningen:
$\frac {3}{80} \cdot 100 \percent = 3,8 \percent$
I femtisonen ligger gjennomsnittsfarten ca 4 % over fartsgrensen.
$ \frac {1}{80} \cdot 100 \percent = 1,3 \percent $
I åttisonen ligger gjennomsnittsfarten drøye en prosent over fartsgrensen.
e)
I femtisonen er det flere som kjører for fort. De fleste av disse kjører bare "litt" for fort. I åttisonen er det ikke så mange som kjørere for fort, men fem av disse kjører mye for fort.
Oppgave 5
a)
b)
1)
2)
c)
d)
Oppgave 6
a)
$29 = 16 + 8 + 4 + 0 + 1 = 2^4 + 2^3 +2^2 + 2^0$
b)
$1 + 0+ 4 + 8 + 16 \\ 25 + 0 + 100 + 200 + 400 = 725 $
c)
Den kan brukes fordi "hoppet" fra en toerpotens til den neste er en dobling.
Oppgave 7
a)
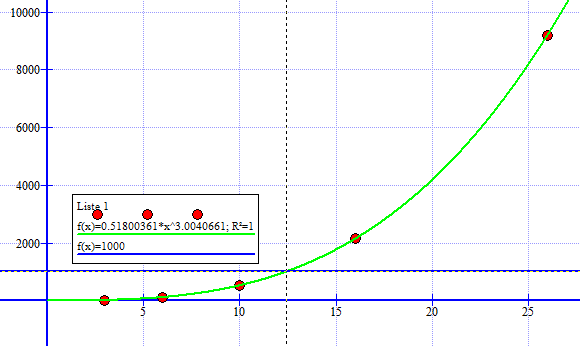
1)
Fra figuren nedenfor ser man at $f(x) = 0,52 \cdot x^{3,0}$ er en god modell for sammenhengen mellom diameter og volum til kulene.
2)
b)
Fra figuren over ser man at diameteren er 12,4 cm. når volumet er 1000ml.
c)
$V = \frac 43 \pi r^3 \\ Diameter \quad = x \\ r = \frac x2 \\ V = \frac 43 \pi ( \frac x2)^3 \\ V = \frac{4 \cdot \pi}{3 \cdot 8}x^3 \\ V = 0,52x^3 $
Dette er i samsvar med modellen i a.