2P 2011 høst LØSNING

MAT 1015

Løsning fra NDLA

DEL EN

Oppgave 1

a)

1) 533 milliarder = 533 000 000 000 = <Math>5,33 \cdot 10^{11}</Math>

2) <math>0,000533 = 5,33 \cdot 10^{-4}</math>

b)

1) <math> 8 \cdot 2^{-2} = 8 \cdot \frac{1}{2^2} = \frac{8 \cdot 1}{4} = 2 </math>

2) <math> 2^3 \cdot (\frac{3}{2})^2 = 8 \cdot \frac{ 9} {4 } = \frac {8 \cdot 9 }{4 } = 2 \cdot 9 = 18</math>

c)

2, 1, 3, 4, 5, 5, 3, 6, 4, 3

Vi ordner i stigende rekkefølge:

1, 2, 3, 3, 3, 4, 4, 5, 5, 6

Median er de to tallene i midten, delt på to. 3 + 4 = 7. Så deler man på to: 7:2 = 3,5

Variasjonsbredden er 6 - 1 = 5, forteller oss bare at hele skalaen er i bruk.

Gjennomsnitt: <Math> \frac{1+2+3+3+3+4+4+5+5+6}{10} = 3,6</Math>

d)

40 000km = 40 000 000m

20cm/ ball = 0,2m/ ball

<math>\frac{4\cdot 10^7}{2 \cdot 10^{-1} } fotballer = 2 \cdot 10^8</math> fotballer.

e)

1)

2)

Alle verdigivene siffer øker med faktoren to, se oppgaven over, derfor blir tallet dobblet når man legger til en null bakerst.

3)

Følger vi systemet over er 24 = 11000 og 48 = 110000.

f)

De svømmer I et 25 meters basseng. Kine er presis i starten og vender først, etter ca 18 sekunder. Mina vender etter ca 25 sekunder og har de siste 10 meterne tapt mye i forhold til Kine. Kine svømmer bra til det er ca 17 meter igjen, da sprekker hun og blir forbisvømt av Mina etter 30 sekunder, 15 meter før mål. Mina kommer i mål etter ca. 46 sekunder og Kine etter ca. 56.

g)


Fart (km/t)	Antall biler	klassemidtpunkt	klassemidtpunkt <Math> \cdot </Math> frekvens
[20,30>	20	25	500
[30,40>	20	35	700
[40,50>	10	45	450
			1650

Gjennomsnitt: 1650:50 = 33 kilometer i timen.

h)

Han har hatt en måned med 5 prosent vekst, to måneder med 0,8 prosent vekst og tre måneder med 15 prosent nedgang.

Oppgave 2


	April	Mai	Juni
Per	225	90	450
Pål	675	180	450
Espen	0	630	900

DEL TO

Oppgave 3

a)

Boken skulle vært levert for hundre år siden, altså er man 5200 uker for sent ute.

Modeller:

Gebyr1 (x) = $ 0,10 + (x-1)\cdot 0,05 $

Gebyr2 (x) = $ 0,10 \cdot 1,002^{x-1} $

Dersom modell 1 betales det: Gebyr1 (5200) = $ 0,10 + (5200-1)\cdot 0,05 = 260kr $

Dersom modell 2 betales det: Gebyr2 (5200) = $ 0,10 \cdot 1,002^{5200-1} = 3246 kr $

b)

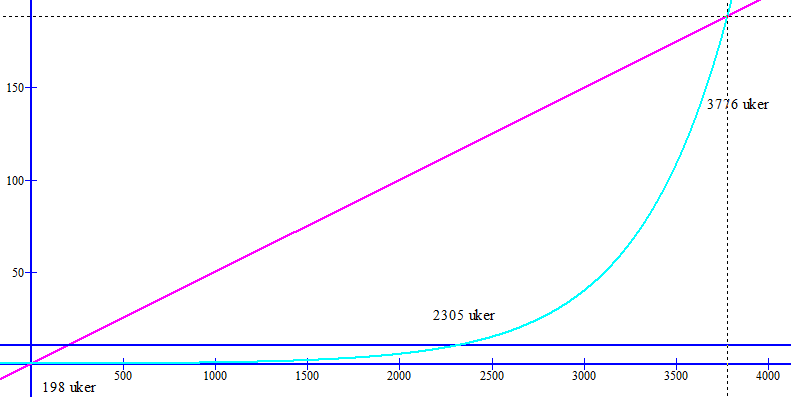
Man observerer at den lineære modellen, modell en først kommer opp i ti kroner, etter ca. 198 uker. Den eksponentielle modellen når ti kroner etter ca. 2305 uker. Modellene gir like store kostnader etter ca. 3776 uker.

Oppgave 4


Årstall	2005	2006	2007
Innbyggertall	225	90	450
Endring fra året før	675	180	450
Prosentvis endring fra året før	0	630	900