2P 2013 vår ny LØSNING
Del 1
Oppgave 1
a)
Finn median:
Sorterer observasjonene:
Finner antall observasjoner:
Finner midtpunktet:
Fordi det er et partall antall observasjoner er medianen lik gjennomsnittet av de to verdiene som ligger på hver sin side av midtpunktet
Medianen er gjennomsnittet av verdiene nummer 5 og 6.
Finner gjennomsnitt:
Finner summen av observasjonsverdiene:
Finner antall observasjoner:
Gjennomsnittet er da:
Finn typetall:
Teller opp verdiene og lager en frekvenstabell:
| Verdi | Frekvens |
|---|---|
Ser i tabellen og finner de hyppigst forekommende verdiene
Typetall(ene) er: 1
b)
| Verdi x | Frekvens f | Kumulativ frekvens |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 2 | 3+2 = 5 |
| 3 | 2 | 5+2 = 7 |
| 4 | 1 | 7+1 = 8 |
| 5 | 2 | 8 + 2 = 10 |
Oppgave 2
Oppgave 3
A:
B:
Fordi
Oppgave 4
a)
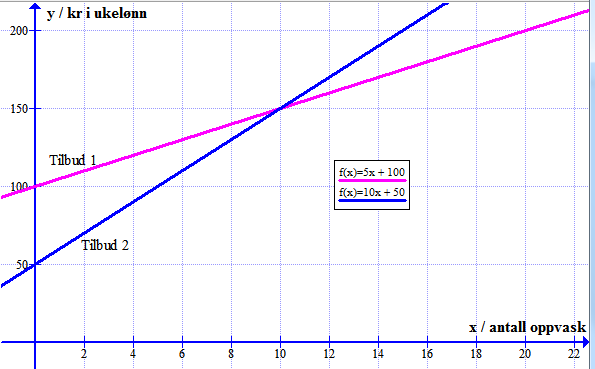
Tilbud 1:
Tilbud 2:
b)
Ettersom dette er del 1 av eksamen, må denne grafen skisseres for hånd, men jeg bruker her Graph
Ser av grafen at det lønner seg for Sigvald med tilbud 1 dersom han vasker opp mindre enn 10 ganger i uka. Vi vet ikke hvor ofte de vasker opp i familien, men hvis de for eksempel vasker opp en gang om dagen, så lønner det seg for Sigvald med Tilbud 1.
Oppgave 5
| Plassverdisystem med grunntall 10 | Plassverdisystem med grunntall 2 |
|---|---|
Konverterer
Konverterer
Oppgave 6
a)
b)
Graf C tilhører f.
Vi ser at graf A er en rett linje, men
Graf C synker raskest i starten, men etterhvert som bilen blir billigere så går den mindre ned i verdi hvert år. Prisen synker med 10% hvert år, og det blir 10% av et mindre og mindre beløp.
Oppgave 7
| Inntekt (i 1000 kroner) | Klassemidtpunkt |
Antall personer |
Klassesum |
Gjennomsnittet er omtrent:
Oppgave 8
Del 2
Oppgave 1
a)
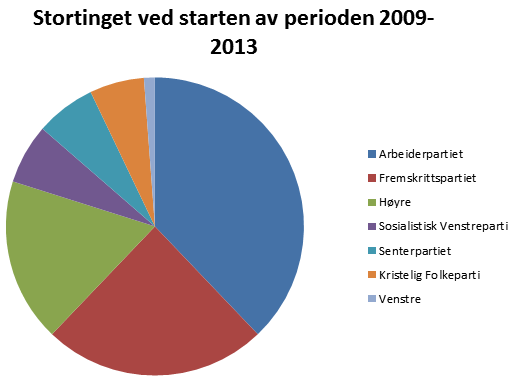
Bruker Excel for å tegne sektordiagrammet..
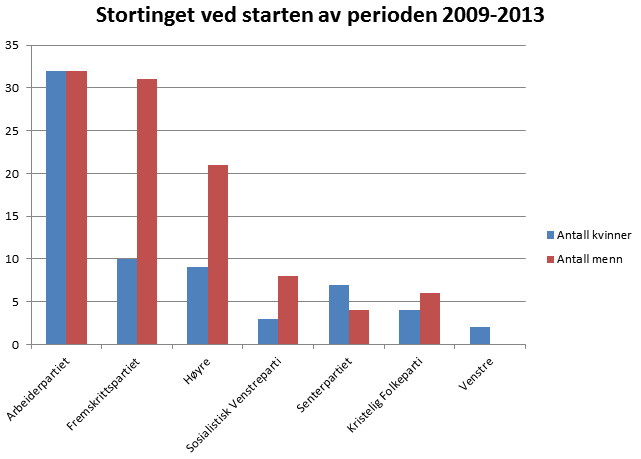
b)
Oppgave 2
Oppgave 3
Oppgave 4
a)
Vinnertid 1968: 123.4
Vinnertid 2010:105,57
Vinnertiden sank med 14% fra 1968 til 2010.
b)
Bruker 2P-kalkulatoren. Funksjon: Verdiliste => Gjennomsnitt.
Gjennomsnitt1968:
Gjennomsnitt 2010: