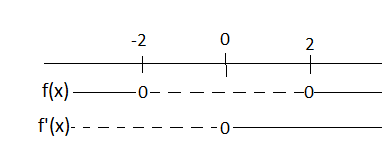1T 2010 vår LØSNING: Forskjell mellom sideversjoner
| Linje 20: | Linje 20: | ||
=== e) === | === e) === | ||
<math>f(x)= -2x^3+8x+4 \ f'(x) = -6x + 8 \ f'(1) = -6+8=2 \ f(1) = 10 \ y= ax+b \ y=2x+b \punktet \quad (1,f(1)) \Rightarrow 10 = 2 + b \ b = 8 \ Likning | <math>f(x)= -2x^3+8x+4 \ f'(x) = -6x + 8 \ f'(1) = -6+8=2 \ f(1) = 10 \ y= ax+b \ y=2x+b \ \text{punktet} \quad (1,f(1)) \Rightarrow 10 = 2 + b \ b = 8 \ \text{Likning for tangent:} y=2x+8</math> | ||
=== f) === | === f) === | ||
Sideversjonen fra 2. mar. 2013 kl. 23:37
Del 1
Oppgave 1
a)
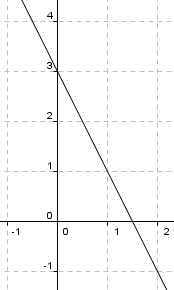
Nullpunkt ved regning:
Ved inspeksjon ser man at dette stemmer med grafen.
b)
c)
d)
e)
f)
Faktoriserer uttrykket ved hjelp av konjugatsetningen og regelen for faktorisering av fullstendig kvadrat, forkorter deretter uttrykket ved å stryke samme faktorer i teller og nevner:
g)
h)
1)
Sannsynligheten for at pilen peker enten på blått eller grønt felt når hjulet stopper er:
2)
Sannsynligheten for at pilen peker en gang på gult felt og en gang på grønt felt når hjulet snurres to ganger, er:
i)
Oppgave 2
a)
b)
Legger sammen de to likningene og får:
8a-8=0
a=1
Innsatt i 4a + 2b- 4 = 0
Gir b=0, funksjonsuttrykket blir da
Del 2
Oppgave 3
a)
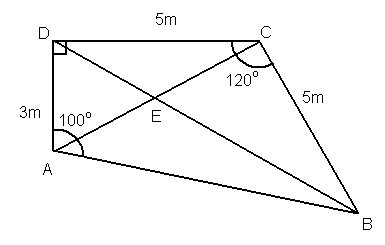
Siden trekant
b)
Cosinussetningen:
c)
Areal trekant ACD:
For å finne arealet av de tre andre trekantene trenger man å finne en del størrelser.
Bruker tangens og finner at:
Vinkel CAD = 59,04 grader
Vinkel DCA = 30,96 grader
Det fører til at
Vinkel BAE = 40,96 grader og
Vinkel ACB = 89,04 grader
Trekanten BCD er likebeint hvilket betyr at vinkel CBE = EDC = 30 grader.
Areal trekant BCD:
Areal trekant ABD:
Areal trekant ABC:
1)
OVE: ABD + BCD =
2)
TOMMY: ABC + ACD =
Oppgave 4
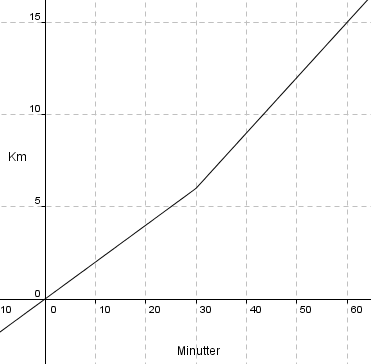
a)
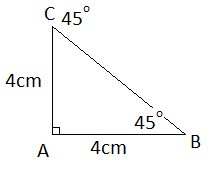
Bruker fartsformelen
b)
c)
Funksjonsuttrykket for de første 30 minuttene er:
Funksjonsuttrykket for de neste 30 minuttene er:
Oppgave 5
a)
Lager krysstabell, setter inn verdiene fra oppgaven og regner ut de andre slik at tabellen blir fullstendig:
| Briller B | Ikke briller |
Sum | |
| Kontaktlinser L | |
|
|
| Ikke kontaktlinser |
|
|
|
| Sum | |
|
|
b)
Som vi regnet ut i tabellen i a) er sannsynligheten for at en person ikke bruker briller
c)
Sannsynligheten for at en person som bruker briller også bruker kontaktlinser er:
Oppgave 6
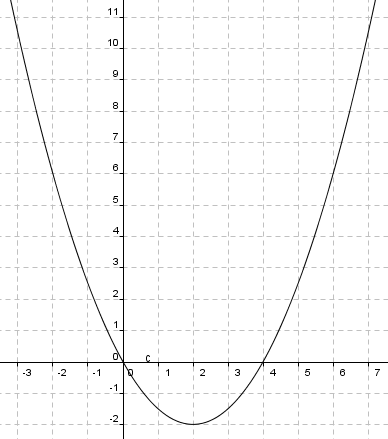
a)
b)
Grafen har nullpunkt når
Altså er
Det stemmer, altså er nullpunktene til funksjonen(på formen
c)
d)
Oppgave 7
Alternativ I
a)
1)
Når a=6, er likningssettet:
Hvis x=0, er
2)
b)
Setter inn x=1 og y=5 i den øverste likningen i likningssettet og løser for a:
c)
Dersom man får null under rottegnet i abc formelen har man en løsning. Dersom man får et negativt tall under rottegnet har man ingen løsning. To løsninger får man når uttrykket under rottegnet er positivt.
Man observerer at når a er større enn 15 er uttrykket negativt og likningsettet har ingen løsning.
Når a = 15 har det en løsning.
Når a er mindre enn 15 har settet to løsninger.
Alternativ II
a)
Vi deler opp arealet i to. Huset består av et kvadrat med areal
og et rektangel med areal
Det totale arealet blir da:
b)
c)
Når a = 7,5m er huset 112,5 kvadratmeter
d)
Huset er større enn 72 kvadrat meter når a er større enn 3m og mindre enn 12m