Cosinussetningen: Forskjell mellom sideversjoner
Fra Matematikk.net
m Teksterstatting – «<tex>» til «<math>» |
m Teksterstatting – «</tex>» til «</math>» |
||
| Linje 1: | Linje 1: | ||
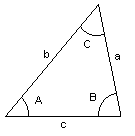
I en trekant med vinkler A, B og C og sider a, b og c (a motstående til A osv.) er | I en trekant med vinkler A, B og C og sider a, b og c (a motstående til A osv.) er | ||
<math>a^2 =b^2+ c^2 -2bc \cdot cosA </ | <math>a^2 =b^2+ c^2 -2bc \cdot cosA </math> | ||
| Linje 7: | Linje 7: | ||
Setningen kalles også den utvidede pytagoreiske læresettning og det går også an å skrive den slik:<br> | Setningen kalles også den utvidede pytagoreiske læresettning og det går også an å skrive den slik:<br> | ||
<math>b^2 =a^2+ c^2 -2ac \cdot cosB </ | <math>b^2 =a^2+ c^2 -2ac \cdot cosB </math><br> | ||
eller slik:<br> | eller slik:<br> | ||
<math>c^2 =a^2+ b^2 -2ab \cdot cosC </ | <math>c^2 =a^2+ b^2 -2ab \cdot cosC </math><br> | ||
Setningen kan brukes på alle trekanter. Legg merke til at setningen kan brukes til å finne vinklene i en trekant dersom alle tre sidene er gitt. | Setningen kan brukes på alle trekanter. Legg merke til at setningen kan brukes til å finne vinklene i en trekant dersom alle tre sidene er gitt. | ||
Sideversjonen fra 5. feb. 2013 kl. 20:58
I en trekant med vinkler A, B og C og sider a, b og c (a motstående til A osv.) er
<math>a^2 =b^2+ c^2 -2bc \cdot cosA </math>
Setningen kalles også den utvidede pytagoreiske læresettning og det går også an å skrive den slik:
<math>b^2 =a^2+ c^2 -2ac \cdot cosB </math>
eller slik:
<math>c^2 =a^2+ b^2 -2ab \cdot cosC </math>
Setningen kan brukes på alle trekanter. Legg merke til at setningen kan brukes til å finne vinklene i en trekant dersom alle tre sidene er gitt.
Eksempel: