Tallregning: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
m Teksterstatting – «<tex>» til «<math>» |
||
| Linje 44: | Linje 44: | ||
*Addisjon + | *Addisjon + | ||
*subtraksjon - | *subtraksjon - | ||
*Multiplikasjon < | *Multiplikasjon <math> \cdot </tex> | ||
*divisjon : | *divisjon : | ||
I tilleg har man påtense og paranteser. | I tilleg har man påtense og paranteser. | ||
*Potens: < | *Potens: <math> a^n</tex>, for eksempel <math> 5^2 = 5 \cdot = 25</tex> | ||
* Parantes: < | * Parantes: <math>(a+b)\cdot c</tex> | ||
På samme måte som andre språk har grammatikk har matematikk også noen regler for hvordan de forskjellige operasjonene skal utføres. | På samme måte som andre språk har grammatikk har matematikk også noen regler for hvordan de forskjellige operasjonene skal utføres. | ||
| Linje 78: | Linje 78: | ||
<blockquote style="padding: 1em; border: 3px dotted red;"> | <blockquote style="padding: 1em; border: 3px dotted red;"> | ||
'''Eksempel'''<p></p> | '''Eksempel'''<p></p> | ||
< | <math> 3(2+3^2)+2(4-2^2)= | ||
\\ 3(2+9)+2(4-4)= \\ 3\cdot11 +0 = 33 </tex> | \\ 3(2+9)+2(4-4)= \\ 3\cdot11 +0 = 33 </tex> | ||
</blockquote> | </blockquote> | ||
<blockquote style="padding: 1em; border: 3px dotted red;"> | <blockquote style="padding: 1em; border: 3px dotted red;"> | ||
'''Eksempel'''<p></p> | '''Eksempel'''<p></p> | ||
< | <math>2+3\cdot 3 (1+2^3)-4\cdot2^2 = \\2+9 (1+8)-4\cdot4 = \\\\2+ 81-16 = 67 | ||
</tex> | </tex> | ||
</blockquote> | </blockquote> | ||
| Linje 177: | Linje 177: | ||
'''Eksempel'''<p></p> | '''Eksempel'''<p></p> | ||
Har vi flere parentesnivåer begynner vi å løse opp parentesene innenifra. <p></p> | Har vi flere parentesnivåer begynner vi å løse opp parentesene innenifra. <p></p> | ||
< | <math>12 - ( 3 + ( 2 - ( - 8 ) + 4 ) - 2 ) +10 = \\ 12 - ( 3 + ( 2 + 8 + 4 ) - 2 ) +10 = \\ | ||
12 -( 3 + 2 + 8 + 4 - 2) + 10 = \\ 12 - 3 - 2 - 8 - 4 + 2 + 10 = 7 </tex> | 12 -( 3 + 2 + 8 + 4 - 2) + 10 = \\ 12 - 3 - 2 - 8 - 4 + 2 + 10 = 7 </tex> | ||
Sideversjonen fra 5. feb. 2013 kl. 20:58
Denne siden behandler grunnleggende emner som regnerekkefølge, fortegn, parenteser og litt om tallmengder og tall. Tegnet ≠ brukes, og det betyr "ikke lik".
Tallsystem
Vi bruker titallsystemet som består av ti siffer, fra 0 til 9. I tillegg er det slik at plasseringen eller posisjonen til sifferet har betydning for verdien av tallet. Slike systemer kalles posisjonssystemer. Det romerske tallsystemet er et eksempel på at ikke alle tallsystemer er posisjonssystemer.
Posisjonssystemet
Eksempelvis betyr sifferet 3, i tallet 321, tre hundrere, mens det samme siffer i tallet 13, betyr tre enere. I tallet 0,2, betyr sifferet 2, to tideler, men i tallet 0,002 betyr det samme sifferet to tusendeler. Et talls størrelse kommer an på sifferests verdi og plassering (posisjon). Derfor er det viktig at man plasserer tallene under hverandre når man skal legge sammen og trekke fra.
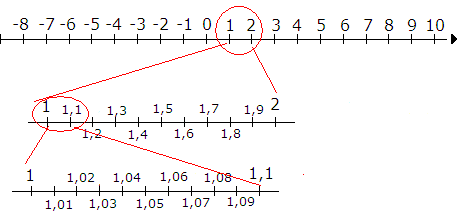
Tallinjen
Tallinjen inneholder uendelig mange tall, derfor er det naturlig å dele dem opp i ”familier”. Vi kaller slike familier for tallmengder. Tallene i en tallmengde har gjerne noe til felles.
Fortegn
Et tall kan ha to typer fortegn, negativt eller positivt. Et negativt tall skrives med et minus foran seg. Alle tall som ligger til høyre for null på tallinjen er positive. Alle tall til venstre for null er negative.
Et positivt tall er et tall med positivt fortegn altså et pluss. Vanligvis skriver vi ikke det positive fortegnet.
Tallene til høyre for null er positive. Til venstre for null på tallinja er tallene negative. Legg merke til at avstanden fra null til for eksempel 5 og -5 er den samme. Det betyr at tallverdien er lik, men fortegnet er forskjellig.
Regnerekkefølge
Når vi regner bruker vi forskjellige symboler for de forskjellige regneoperasjoner som addisjon, subtraksjon, multiplikasjon og divisjon. Symbolene er:
- Addisjon +
- subtraksjon -
- Multiplikasjon <math> \cdot </tex>
- divisjon :
I tilleg har man påtense og paranteser.
- Potens: <math> a^n</tex>, for eksempel <math> 5^2 = 5 \cdot = 25</tex>
- Parantes: <math>(a+b)\cdot c</tex>
På samme måte som andre språk har grammatikk har matematikk også noen regler for hvordan de forskjellige operasjonene skal utføres. Regneoperasjonene utføres i denne rekkefølgen:
- Potenser
- Paranteser
- Multiplikasjon og divisjon
- Addisjon og subtraksjon
De fleste fei gjøres fordi elever regner direkte fra venstre mot høyre uten å ta hensyn til regnerekkefølgen:
Eksempel
5+2 · 10 = 25
5 + 2 ·10 ≠ 70
Mange elever tror at regnestykket over blir 70. Slik er det ikke fordi multiplikasjon utføres først (selv om addisjonstegnet kommer før multiplikasjonstegnet). SJEKK KALKULATOREN, mange kalkulatorer regner feil her!
Eksemplet over kan overstyres med paranteser, fordi parantesene forteller oss i hvilken rekkefølge ting skal skje.
Eksempel
5+2 · 10 = 25
Dersom man skriver stykket slik
(5+2) · 10 =
Da har man fått et helt annet regnestykke fordi parantesen forteller oss at det som er i den skal regnes ut før vi ganger. Stykket blir da:
(5+2) · 10 = (7)· 10 = 7· 10 = 70
Ved å bruke paranteser kan man styre regnerekkefølgen. Å skrive 5+(2 · 10) er unødvendig fordi multiplikasjon alltid kommer før addisjon.
Eksempel
<math> 3(2+3^2)+2(4-2^2)= \\ 3(2+9)+2(4-4)= \\ 3\cdot11 +0 = 33 </tex>
Eksempel
<math>2+3\cdot 3 (1+2^3)-4\cdot2^2 = \\2+9 (1+8)-4\cdot4 = \\\\2+ 81-16 = 67 </tex>
Negative tall
Addisjon
3 + 2 = 5
3 + 1 = 4
3 + 0 = 3
3 + ( - 1 ) = 2
3 + ( - 2 ) = 1
3 + ( - 3 ) = 0
3 + ( - 4 ) = - 1
3 + ( - 5 ) = - 2
osv.
Fra tabellen ser vi at å addere et positivt og et negativt tall er det samme som å trekke fra tilsvarende positivt tall. [ 3 + ( - 2 ) = 1 og 3 - 2 = 1 ].
Subtraksjon
3 - 2 = 1
3 - 1 = 2
3 - 0 = 3
3 - ( - 1 ) = 4
3 - ( - 2 ) = 5
osv.
å subtrahere et negativt tall er det samme som å legge til tilsvarende positive tall.
Multiplikasjon
Når vi multipliserer et positivt og et negativt tall blir svaret negativt.
(-5) · 10 = - 50
Når vi multipliserer to negative tall blir svaret positivt.
(-5) · (-10) = 50
Divisjon
Når vi dividerer et negativt og et positivt tall blir svaret negativt.
5 : (-10) = - 1/2
Når vi dividerer to negative tall blir svaret positivt.
(-5) : (-10) = 1/2
Parenteser
Når vi løser opp en parentes med positivt fortegn beholder vi fortegnene inne i parentesen. Eks.
12 + ( -2 + 4 -1) = 12 - 2 + 4 -1 = 13
Når vi løser opp en parentes med negativt fortegn må vi skifte alle fortegnene inne i parentesen. Eks. 12 - ( - 2 + 4 - 1 ) = 12 + 2 - 4 + 1 =11
Eksempel
Har vi flere parentesnivåer begynner vi å løse opp parentesene innenifra.
<math>12 - ( 3 + ( 2 - ( - 8 ) + 4 ) - 2 ) +10 = \\ 12 - ( 3 + ( 2 + 8 + 4 ) - 2 ) +10 = \\ 12 -( 3 + 2 + 8 + 4 - 2) + 10 = \\ 12 - 3 - 2 - 8 - 4 + 2 + 10 = 7 </tex>
Huskeregler
- Like tegn blir pluss (++ og --).
- Ulike tegn blir minus (+- og -+).
- Når du løser opp en parentes med minus foran, skifter du fortegn på alle tallene inne i parentesen.
Dersom du synes dette er vanskelig kan du jo tenke litt på ordenes betydning og så trekke parallellen over til matematikk.
- " I love you!" + positiv betydning
- " I do not love you" - negativ betydning
- " I love you. Not!" + og - gir negativ betydning.
- " I do not love you. Not!" - og - gir en positiv betydning.
(NB: Dette er ikke god engelsk)