Skalarprodukt: Forskjell mellom sideversjoner
Ingen redigeringsforklaring |
m Teksterstatting – «<tex>» til «<math>» |
||
| Linje 1: | Linje 1: | ||
Et skalarprodukt er en regneoperasjon (multiplikasjon) mellom to vektorer. Skalarproduktet er et såkalt [[indreprodukt]]. Resultatet av regneoperasjonen er et reelt tall. Tallet bestemmes av lengden på vektorene og vinkelen mellom dem. | Et skalarprodukt er en regneoperasjon (multiplikasjon) mellom to vektorer. Skalarproduktet er et såkalt [[indreprodukt]]. Resultatet av regneoperasjonen er et reelt tall. Tallet bestemmes av lengden på vektorene og vinkelen mellom dem. | ||
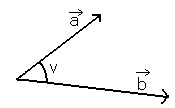
Vinkelen v mellom vektorene skal være element i intervallet [0°,180°]. Vi har vektorene < | Vinkelen v mellom vektorene skal være element i intervallet [0°,180°]. Vi har vektorene <math>\vec{a}</tex> og <math>\vec{b}</tex>. | ||
[[bilde:skalar.gif]] | [[bilde:skalar.gif]] | ||
| Linje 7: | Linje 7: | ||
Skalarproduktet defineres som: | Skalarproduktet defineres som: | ||
< | <math>\vec{a}\cdot \vec{b} = |\vec{a}|\cdot |\vec{b}| cos(v)</tex> | ||
| Linje 13: | Linje 13: | ||
og leses "a vektor prikk b vektor er lik lengden av a vektor multiplisert lengden av b vektor multiplisert cosinus til vinkelen mellom dem". | og leses "a vektor prikk b vektor er lik lengden av a vektor multiplisert lengden av b vektor multiplisert cosinus til vinkelen mellom dem". | ||
Vektorene skrives av og til med fete typer og andre ganger med en liten pil over. Som man ser er det ikke konsekvens, man bør kjenne begge. På samme måte er det med lengden av en vektor, du vil støte på både |< | Vektorene skrives av og til med fete typer og andre ganger med en liten pil over. Som man ser er det ikke konsekvens, man bør kjenne begge. På samme måte er det med lengden av en vektor, du vil støte på både |<math>\vec{v}</tex>| og ||<math>\vec{v}</tex>|| som notasjon, men begge betyr altså lengden av vektoren v. | ||
== Koordinatform == | == Koordinatform == | ||
| Linje 19: | Linje 19: | ||
I et ortonormert koordinatsystem har vi følgende i planet: | I et ortonormert koordinatsystem har vi følgende i planet: | ||
Dersom vektoren < | Dersom vektoren <math>\vec{a} = [x_a,y_a]</tex> og vektor <math>\vec{a} = [x_b,y_b]</tex> har vi at | ||
< | <math>\vec{a}\cdot \vec{b} = x_ax_b+y_ay_b</tex> Eksempelvis, dersom <math>\vec{a}</tex> = [1,5] og <math>\vec{b}</tex> = [-2,3] er skalarproduktet: | ||
[1,5] · [-2,3] = -2 + 15 = 13 | [1,5] · [-2,3] = -2 + 15 = 13 | ||
| Linje 27: | Linje 27: | ||
===I rommet=== | ===I rommet=== | ||
Vektorene < | Vektorene <math>\vec{a}= [x_a,y_a,z_a]</tex> og <math>\vec{b}= [x_b,y_b,z_b]</tex> gir skalarprodukt: | ||
< | <math>\vec{a}\cdot \vec{b} = x_ax_b+y_ay_b+a_zb_z</tex> | ||
| Linje 42: | Linje 42: | ||
I fysikken brukes skalarproduktet i definisjonen av arbeid: | I fysikken brukes skalarproduktet i definisjonen av arbeid: | ||
< | <math>W=\vec{F}\cdot\vec{s}</tex> | ||
[[Category:vektor]][[Category:ped]][[Category:1T]] | [[Category:vektor]][[Category:ped]][[Category:1T]] | ||
[[kategori:lex]] | [[kategori:lex]] | ||
Sideversjonen fra 5. feb. 2013 kl. 20:58
Et skalarprodukt er en regneoperasjon (multiplikasjon) mellom to vektorer. Skalarproduktet er et såkalt indreprodukt. Resultatet av regneoperasjonen er et reelt tall. Tallet bestemmes av lengden på vektorene og vinkelen mellom dem.
Vinkelen v mellom vektorene skal være element i intervallet [0°,180°]. Vi har vektorene <math>\vec{a}</tex> og <math>\vec{b}</tex>.
Skalarproduktet defineres som:
<math>\vec{a}\cdot \vec{b} = |\vec{a}|\cdot |\vec{b}| cos(v)</tex>
og leses "a vektor prikk b vektor er lik lengden av a vektor multiplisert lengden av b vektor multiplisert cosinus til vinkelen mellom dem".
Vektorene skrives av og til med fete typer og andre ganger med en liten pil over. Som man ser er det ikke konsekvens, man bør kjenne begge. På samme måte er det med lengden av en vektor, du vil støte på både |<math>\vec{v}</tex>| og ||<math>\vec{v}</tex>|| som notasjon, men begge betyr altså lengden av vektoren v.
Koordinatform
I planet
I et ortonormert koordinatsystem har vi følgende i planet:
Dersom vektoren <math>\vec{a} = [x_a,y_a]</tex> og vektor <math>\vec{a} = [x_b,y_b]</tex> har vi at
<math>\vec{a}\cdot \vec{b} = x_ax_b+y_ay_b</tex> Eksempelvis, dersom <math>\vec{a}</tex> = [1,5] og <math>\vec{b}</tex> = [-2,3] er skalarproduktet:
[1,5] · [-2,3] = -2 + 15 = 13
I rommet
Vektorene <math>\vec{a}= [x_a,y_a,z_a]</tex> og <math>\vec{b}= [x_b,y_b,z_b]</tex> gir skalarprodukt:
<math>\vec{a}\cdot \vec{b} = x_ax_b+y_ay_b+a_zb_z</tex>
Praktisk bruk
Normale linjer
Skalarproduktet er egnet til å finne ut om to vektorer står vinkelrett på hverandre. Dersom vektorene a og b har lengder forskjellig fra null står vektoren normalt på hverandre vis og bare vis skalarproduktet er null.
a · b = 0
Arbeid
I fysikken brukes skalarproduktet i definisjonen av arbeid:
<math>W=\vec{F}\cdot\vec{s}</tex>