1T 2012 høst LØSNING

Oppgave 1

a = -2 og punkt. (3,0)

<tex>0 = -2 \cdot 3 + b \\ b= 6 \\ dvs: \\ y=-2x+6</tex>

Oppgave 2

<tex>lg(2x+3) = 1 \\ 10^{lg(2x+3)} = 10^1 \\ 2x+3 =10 \\ x= \frac 72</tex>

Oppgave 3

<tex>\frac{(2x)^3x^2}{2^5x^{-1}} = 2^{3-5}x^{3+2+1}= \frac{x^6}{4}</tex>

Oppgave 4

<tex>\frac{x^2+6x+9}{x^2-9} = \frac{(x+3)(x+3)}{(x+3)(x-3)} = \frac{x+3}{x-3}</tex>

Oppgave 5

<tex> (\sqrt2 + \sqrt8)^2 = 2+2\sqrt2\sqrt8+8 = 18</tex>

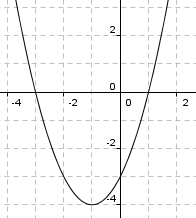
Oppgave 6

a)

Nullpunkter:

f(x) = 0

<tex> x^2+2x-3 =0 \\ x= \frac{-2 \pm\sqrt{4+4 \cdot 3}}{2} \\ x=-3 \quad \vee \quad x=1</tex>

b)

<tex>f'(x) = 2x+2 \\ f'(x) = 0 \\ x= -1 \\ f(-1)=-4</tex>

f har et ekstremalpunkt i (-1,-4). Dette er et minimumspunkt da den deriverte er negativ for verdier mindre enn -1, og positiv for større verdier.

c)

Oppgave 7

<tex>(x+5)(x+3)-(x+5)82x+7)=0 \\ (x+5)(x+3-2x-7)=0 \\ (x+5)=0 \quad \vee \quad -x-4=0 \\ x=-5 \quad \vee \quad x=-4</tex>

Oppgave 8

	Sommerjobb S	Ikke sommerjobb <tex>\bar{S}</tex>	Sum
Ferie F	<tex>10</tex>	<tex>4-2=2</tex>	<tex>10+2=12</tex>
Ikke ferie <tex>\bar{F}</tex>	<tex>16-10=6</tex>	<tex>2</tex>	<tex>6+2=8</tex>
Sum	<tex>16</tex>	<tex>20-16=4</tex>	<tex>20</tex>