1T 2011 høst LØSNING

DEL EN

a)

<tex> \frac{x^2-25}{x^2+10x+25} = \frac{(x+5)(x-5)}{(x+5)(x+5)} = \frac{x-5}{x+5}</tex>

b)

<tex> 3^{2x-1} = 1 \\ 3^{2x-1} = 3^0 \\ 2x-1 = 0 \\ x= \frac 12</tex>

c)

<tex> \frac{a^{\frac 14} \sqrt a}{(a^{\frac 34})^3 \cdot a^{-2}}= a^{\frac 14 + \frac 24 - \frac 94 + \frac 84} = a^{\frac 12} = \sqrt a </tex>

d)

<tex> A= \frac {gh}{2} \\6= \frac {5h}{2} \\ h = \frac {12}{5} </tex>

e)

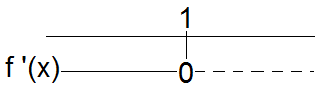
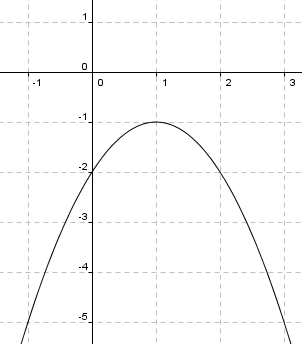
Ser fra figuren at:

<tex> f(x) \leq 0 \quad \quad \quad x \in <\leftarrow,1] \cup [3, \rightarrow> \\ f(x) > g(x) \quad \quad x \in <0,5></tex>

f)

<tex>tanC =2 \\ 2= \frac{AB}{AC} \\ AC = 1,5 </tex>

g)

3 Blå, 2 røde, 1 grønn. Totalen er 6.

1) <tex> \frac 56 \cdot \frac 45 = \frac 23 </tex>

2) <tex> \frac 36 \cdot \frac 25 + \frac 26 \cdot \frac 35 = \frac 25 </tex>

h)

<tex> f(x)=x^2+1 \\ \lim_{\Delta x\to\0}\quad\frac{f(x+ \Delta x) - f(x)}{\Delta x} \\ \lim_{\Delta x\to\0}\quad\frac{(x+ \Delta x)^2 +1 - (x^2+1)}{\Delta x} \\ \lim_{\Delta x\to\0}\quad\frac{x^2+2x \Delta x +( \Delta x)^2+1-x^2-1 }{\Delta x} \\ \lim_{\Delta x\to\0}\quad\frac{2x \Delta x +( \Delta x)^2}{\Delta x} \\ \lim_{\Delta x\to\0}\quad\frac{\Delta x(2x + \Delta x)}{\Delta x} \\ \lim_{\Delta x\to\0} \quad 2x + \Delta x = 2x</tex>

a)

<tex>f(x) = -x^2+2x-2</tex>

Desom ingen nullpunkter må

<tex>b^2-4ac <0 \\ 2^2-4 \cdot(-1) \cdot (-2) =-4</tex>

Dvs. ingen nullpunkter

b)

<tex>f'(x) = -2x+2 \\ f'(x)=0 \\ -2x+2 =0 \\ x=1</tex>

Ekstremalpunkt: f(1) = -1, dvs. man har et maksimum i punktet (1,-1).

c)

f har en tangent i (2,-2)

Stigningstall: f'(2)= -2

y=-2x+b

-2 = -4 + b

b=2

Likning for tangent: y = -2x +2

a)

Tilnærmet: F = 2C + 30

Eksakt: 5F = 9C + 160

100 grader celsius er tilnærmet F = 230, altså 230 Farenheit. Eksakt er det:

<tex> 5F = 9C +160 \\ 5F = 900 + 160 \\ F= 212</tex>

Man observerer at forskjellen er 18 grader og at den tilnærmede metoden viser for mye ved 100 grader celsius.

b)

<tex> \left[F=2C+30 \\ 5F = 9C +160 \right] \\ \left[F=2C+30 \\ 5(2C+30) = 9C +160 \right] \\C = 10 \wedge F = 50</tex>

Det betyr at tilnærmingen er helt riktig når temperaturen er 10C (50F), men at den blir mer og mer unøyaktig når temperaturen fjerner seg fra 10 grader celsius.

DEL TO

a)

Dersom trekanten er rettvinklet må siden på 6cm være hypotenus.

<tex>(6cm)^2 \neq (4cm)^2 + (5cm)^2 \\ 36cm^2 \neq 41cm^2 </tex>

Trekanten er ikke rettvinklet.

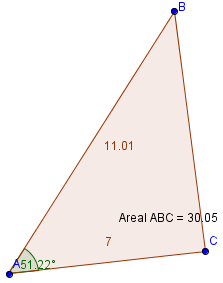
b)

a = 4,0 cm

b = 5,0 cm

c = 6,0 cm

<tex> a^2 = b^2 + c^2 - 2bcCosA \\ Cos A = \frac{16-25-36}{-2 \cdot 5 \cdot 6} = 0,75 \\ A = 41,4 ^{\circ}\\ Areal: \quad A = \frac 12 bcSinA = \frac 12 \cdot 5 \cdot 6 sin 41,4^{\circ} \\ A= 9,9cm^2 </tex>

c)

<tex> A= \frac 12 abSinC </tex>

sinC har et maksimum for c = 90 grader, dvs. sinC=1.

== d) ==

a)

Det var 6000 liter i tanken.

1,000 - 0,864 = 0,136 = 13,6%

b)

c)

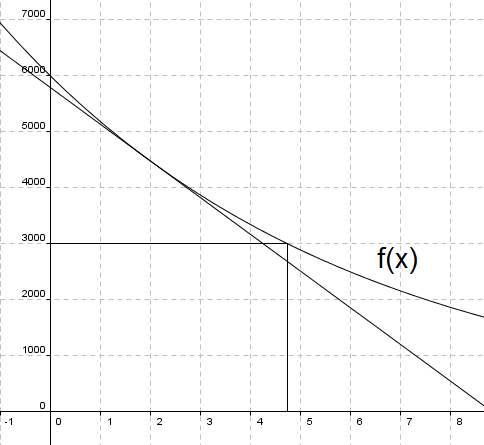
Fra grafen kan man lese at det tar ca. 4 timer og 45 minutter.