R1 2012 vår LØSNING

Oppgave 1:

a)

1)

<tex>f(x) = 5x^3+x-4 \\ f'(x) = 3 \cdot 5x^2 + 1 \\ f'(x) = 15x^2 + 1 </tex>

2)

<tex>g(x) = 5e^{3x} \\ u = 3x \wedge u' = 3 \\ g'(x) = 5e^u \cdot u' \\ g'(x) = 15e^{3x}</tex>

b)

<tex> 2ln(\frac{a^2}{b}) + ln (a \cdot b) - 3ln a = \\ 2ln a^2 - 2ln b + ln a + lnb - 3 lna = \\4ln a - 2ln b + ln a + lnb - 3 lna = \\ 2lna - lnb </tex>

c)

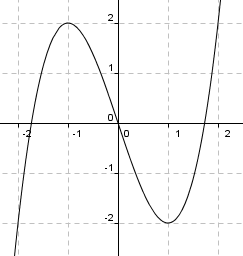
<tex> f(x)= x^3-3x</tex>

1)

Nullpunkter:

<tex>x^3-3x = x(x^2-3)= x(x- \sqrt 3 )(x + \sqrt 3) \\x = - \sqrt3 \quad \vee \quad x = 0 \quad \vee \quad x= \sqrt3</tex>

2)

<tex>f'(x) = 3x^2-3 \\f'(x) = 0 \\ 3(x^2-1) = 0 \\ x = -1 \quad \vee \quad x = 1 \\ f(-1)= 2 \quad \vee \quad f(1) = -2</tex>

Toppunkt (-1,2)

Bunnpunkt (1,-2)

3)