1T 2011 vår LØSNING: Forskjell mellom sideversjoner
| Linje 177: | Linje 177: | ||
<p></p> | <p></p> | ||
b)<p></p> | b)<p></p> | ||
<tex> tan \alpha = \frac {9}{12} \ \alpha = tan^{-1} ( \frac {9}{12}) \ \alpha = 36,9^{\ | <tex> tan \alpha = \frac {9}{12} \ \alpha = tan^{-1} ( \frac {9}{12}) \ \alpha = 36,9^{\circ}</tex> | ||
== Oppgave 6: == | == Oppgave 6: == | ||
Sideversjonen fra 6. mar. 2012 kl. 06:43
Del 1
Oppgave 1
a)
1) <tex>36 200 000 = 3.62 \cdot 10^7</tex>
2) <tex>0.034 \cdot 10^{-2} = 3.4 \cdot 10^{-4}</tex>
b)
<tex>x^2 + 6x = 16 \quad \Leftrightarrow \quad x^2 + 6x - 16 = 0</tex>
Ved fullstendig kvadrat:
<tex>
<tex>x = 2 \quad \vee \quad x = -8</tex>
Eller med abc-formelen:
<tex>x = \frac{-6 \pm \sqrt{6^2 - 4\cdot 1 \cdot (-16)} }{2 \cdot 1} = \frac{-6 \pm \sqrt{100}}{2} = -3 \pm 5</tex>
<tex>x = 2 \quad \vee \quad x = -8</tex>
c)
Begynner med å faktorisere uttrykket:
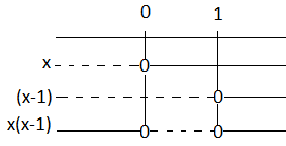
<tex>x^2-x<0 \Leftrightarrow x(x-1)<0 </tex>
Tegner så fortegnsskjema:
<tex>x \in <0,1></tex>
d)
1) E
2) C
3) J
4) B
5) G
6) H
e)
<tex>\text{lg}(2x - 1) = 2</tex>
<tex>2x - 1 = 10^2</tex>
<tex>2x = 101</tex>
<tex>x = \frac{101}{2}</tex>
f)
1)
Lager krysstabell, setter inn verdiene fra oppgaven og regner ut de andre slik at tabellen blir fullstendig:
| Sommerjobb S | Ikke sommerjobb <tex>\bar{S}</tex> | Sum | |
| Ferie F | <tex>10</tex> | <tex>4-2=2</tex> | <tex>10+2=12</tex> |
| Ikke ferie <tex>\bar{F}</tex> | <tex>16-10=6</tex> | <tex>2</tex> | <tex>6+2=8</tex> |
| Sum | <tex>16</tex> | <tex>20-16=4</tex> | <tex>20</tex> |
2)
I tabellen fant vi at 12 elever skal på ferie, og fra oppgaveteksten vet vi at det er 20 elever i klassen. Da blir sannsynligheten for at en tilfeldig valgt elev i klassen skal på ferie <tex>\frac{12}{20}=\frac 35=0,60=60 \percent</tex>
Oppgave 2
a)
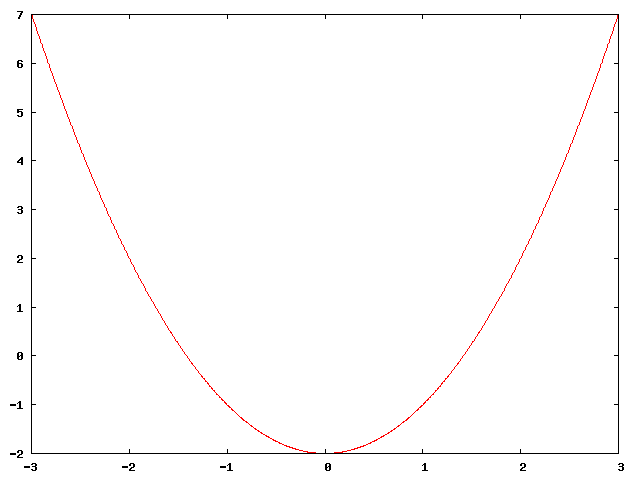
b)
Sekanten er gitt ved
<tex>
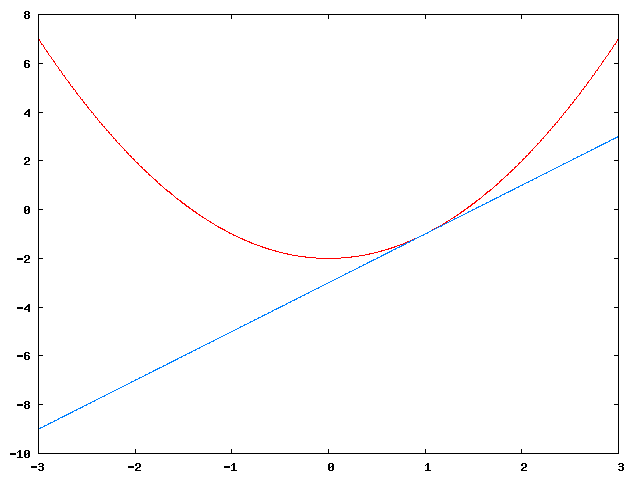
c)
Tangenten er gitt ved
<tex>
Der det er brukt at <tex>f^{\prime}(x) = 2x</tex>.
Oppgave 3
a)
Her er <tex>AB=1</tex>, og <tex>BE=\frac 12 \cdot BC= \frac 12\cdot 1=\frac 12</tex>. Lengden av <tex>AE</tex> blir da:
<tex>AE^2=AB^2+BE^2 \Leftrightarrow AE=\sqrt{AB^2+BE^2}=\sqrt{1^2+\left( \frac 12\right)^2}=\sqrt{(\frac 22)^2+\left( \frac 12\right)^2}=\sqrt{\frac {2^2}{2^2}+\frac {1^2}{2^2}}=\sqrt{\frac{4+1}4}=\sqrt{\frac{5}4}=\frac {\sqrt{5}}{\sqrt{4}}=\frac{\sqrt 5}2</tex>
b)
Areal av trekant AEF:
<tex> A = 1 - 2\frac{1\cdot \frac{1}{2}}{2} - \frac{(\frac{1}{2})^2}{2} = \frac 88 - \frac 48 - \frac 18 = \frac 38</tex>
c)
<tex>A= \frac12 abSinC \ \frac 38 = \frac 12 \cdot \frac{\sqrt5}{2} \cdot \frac{\sqrt5}{2}SinA \ \frac38 = \frac 58 SinA \Sin A = \frac35</tex>
Del 2
Oppgave 4
a)
b)
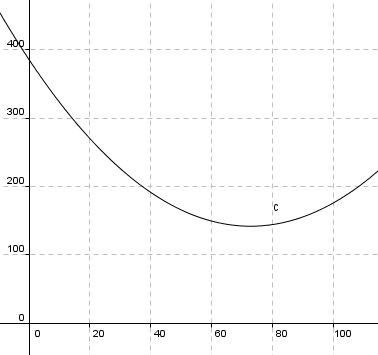
Grafisk:
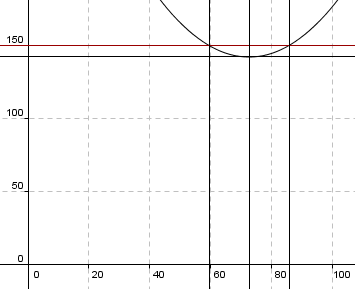
1) Man ser fra grafen at når bilen slipper ut 150g/km er farten enten 60 km/t eller 86km/t.
2) Man ser fra grafen at det laveste utslippet er 142g/km, da er farten 73km/t
Ved regning:
1)
<tex>f(x)=150 \ 0,046x^2-6,7x + 386 = 150 \ 0,046x^2-6,7x + 236 = 0 \ x = \frac{6,7 \pm \sqrt{6,7^2-4 \cdot 0,046 \cdot 236}}{2 \cdot 0,046} = \frac{6,7 \pm 1,21}{0,092}\ x =59,7 \quad \vee \quad x = 86</tex>
2)
<tex>f'(x)=0,092x-6,7 \ f'(x)=0 \ 0,092x - 6,7 = 0 \ x = 72,8 </tex>
c)
<tex>f(70) = 0.046 \cdot 70^2 - 6,7 \cdot 70 +386 = 142,4 </tex>
På en halv time i 70 km/t beveger bilen seg 35km.
Utslippet blir da 4984 gram, altså ca 5kg.
Oppgave 5:
a)
<tex> \frac{1,2}{1,6} = \frac {x}{12} \ x= \frac {x \cdot 1,6}{12 \cdot 1,2} \ x = 9</tex>
b)
<tex> tan \alpha = \frac {9}{12} \ \alpha = tan^{-1} ( \frac {9}{12}) \ \alpha = 36,9^{\circ}</tex>
Oppgave 6:
a)
1)Det var ca. 15 grader. (fra graf der den krysser y aksen)
2)Det ble varemet i ca. 5 minutter og var 90 grader når de ble satt i kjøleskepet.
b)
Grafen for oppvarming, fra null til fem minutter ser ut som en rett linje.:
f(x) = 15x + 15
f(x)= 100
15x + 15 = 100
Det vil ta 5 minutter og 40 sekunder.
c)
<tex> f(x) = 115,82 \cdot 0,94^x x \geq \ f(x)> 60 \ 115,82 \cdot 0,94^x + 5 > 60 \ 0,94^x > 0,4748 \ xlg0,94 > lg 0,4748 \ x < \frac{lg 0,4748}{lg 0,94} \ x \in [5,12> </tex>
d)
5 grader.
Oppgave 7:
a)
| LARS | BÅRD | Resultat |
| papir | papir | U |
| saks | saks | U |
| stein | stein | U |
| stein | saks | V - Lars |
| papir | stein | V - Lars |
| saks | papir | V - Lars |
| papir | saks | V - Bård |
| stein | papir | V - Bård |
| saks | stein | V - Bård |
b)
Fra tabellen i a ser man at det er tre gunstige utfall for at Bård vinner, av ni mulige utfall. 3/9 = 1/3. Dvs. P(B) = 1/3.
Oppgave 8:
a)
<tex>AC=BD \wedge AB=CD \wedge AD = BC \ AC \cdot BC = AB \cdot CD + AD \cdot BC \ AC^2 = AB^2 + AD^2 </tex>
Det er Pytagoras setning.
b)
Likesidet trekant: AB = BC = AC
<tex>AB \cdot PC = AP \cdot BC + PB \cdot AC \ AB \cdot PC = AP \cdot AB + PB \cdot AB \ PC= PA + PB</tex>