Figurer i rommet

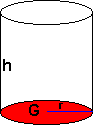
Volum og Overflate

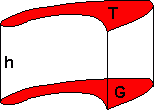
Dersom grunnflaten G og toppflaten T er to parallelle, kongruente plan er volumet gitt ved:

V = Grunnflate · høyde = G · h

Legemets overflate er gitt ved:

O = 2 · Grunnflate + Omkrets Av Grunnflate · høyde

Terning

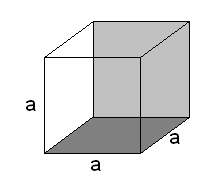
En terning, eller kube, er en romfigur som avgrenses av seks kvadratiske flater. Alle sidekantene har derfor samme lengde. Dersom sidekantene av terningen er lik a, kan terningen se slik ut:

Overflaten av en terning blir summen av de seks kvadratenes areal:

<tex>O = 6a^2</tex>

Eks:

En terning har sidekanter seks centimeter. Hva er overflaten av terningen?

<tex>O = 6 \cdot (6cm)^2 = 216cm^2</tex>

Eks:

En tening har en overflate på <tex>432cm^2</tex>. Hvor lange er sidekantene i terningen?

<tex>O = 6a^2 \Rightarrow a = \sqrt{\frac O6} = \sqrt{ \frac{432cm^2}{6}}= 8,5cm</tex>

Volumet av en terning er lengde ganger bredde ganger høyde. Siden disse har samme lengde kan vi skrive volumet som:

<tex>V = a\cdot a \cdot a = a^3</tex>

Eks:

Sidekantene i en terning er 2cm. Hva er volumet av terningen?

<tex>V = a\cdot a \cdot a = a^3 = (2cm)^3 = 8cm^3</tex>

Eks

En kube har et volum på <tex>125cm^3</tex>. Hva er lengden av en sidekant?

<tex>V = a\cdot a \cdot a = a^3 \Rightarrow a= \sqrt[3] V = \sqrt[3]{125cm^3}= 5cm</tex>

Test deg selv

Prisme

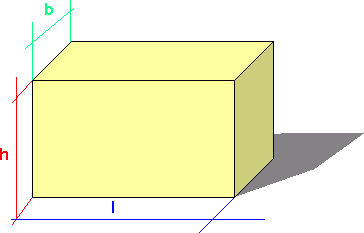
Et prisme er en romfigur der grunnflate og toppflate er like, og med rektangulære sideflater som står vinkelrett på grunnflaten. Det finnes altså prismer med svært forskjellig form. Et rett firkantet prisme kan se slik ut:

Arealet av prismets grunnflate er lengde gange bredde. Når vi multipliserer arealet av grunnflaten med høyden, finner vi volumet.

Grunnflate = lengde · bredde = l · b

Volum : V = Grunnflate · h = l · b · h

Eks:

Et rett prisme har siden 4cm, 10cm og 20cm. Hva er volumet av prismet?

V = Grunnflate · h = l · b · h vi får:

<tex> V = l \cdot b \cdot h = 4cm \cdot 10cm \cdot 20cm = 800cm^3</tex>

(Hva man kaller for bredde, lengde og høyde spiller egentlig ingen rolle, for et rett firkantet prisme. Det kommer jo an på hvordan prismet står eller ligger. Grunnflaten er den siden som vender ned mot jorden)

Eks:

Volumet av et rett firkantet prisme er 200 kubikkcentimeter. Høyden er 5 cm og bredden er 2cm. Hva er lengden av prismet?

<tex>V = l \cdot b \cdot h \Rightarrow l = \frac{V}{bh}= \frac{200cm^3}{2cm \cdot 5cm} = 20cm</tex>

Et rett firkantet prisme er avgrenset av flater hvor to og to er like. Overflaten blir:

Overflate: O = 2lb + 2lh + 2bh

Et firkantet prisme har høyden 12cm. Sidene i grunnflaten er henholdsvis 10cm og 20 cm. Hva er overflaten av prismet?

Siden to og to sider er like store får vi:

<tex> O = 2 \cdot 10cm \cdot 20cm + 2 \cdot 10cm \cdot 12cm + 2 \cdot 20cm \cdot 12cm = 400cm^2 + 240cm^2 + 480cm^2 = 1120cm^2</tex>

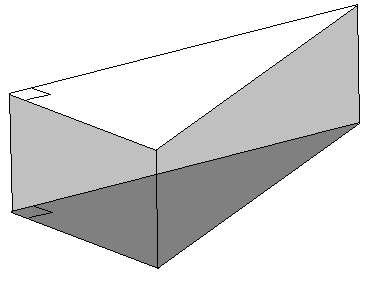
Dette er også et prisme:

Test deg selv

Sylinder

Volum:

<tex>V = Gh= \pi \cdot r^2 \cdot h </tex>

Eks:

En sylinder har høyde 20 cm og radius 5cm. Hva er volumet?

<tex>V = Gh= \pi \cdot r^2 \cdot h = \pi \cdot (5cm)^2 \cdot 20cm = 1570,8 cm^3 = 1,57 dm^3 = 1,57 liter </tex>

Overflate:

<tex> O = 2 \cdot \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot h </tex>

Man regner her med at sylinderen har et lokk, altså en overflate på toppen også. Dersom den ikke har det blir overflaten:

<tex> O = \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot h </tex>

<tex> O = \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot h </tex>

Test deg selv

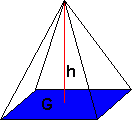
Pyramide

Volum:

<tex>V= \frac 13 Gh </tex>

Eksempel

En pyramide har en rektangulær grunnflate med sider 4,0 cm og 2,0cm. Høyden er 10,0 cm. Hva er volumet av pyramiden?

<tex>V= \frac 13 Gh = \frac 13 \cdot (4,0 cm \cdot 2,0 cm)\cdot 10,0 cm = 26,7cm^3 </tex>

Eksempel

En pyramide har høyde 12,0cm. Volumet er <tex>30 cm^3</tex>. Grunnflaten er et kvadrat. Hvor lang er en side i kvadratet?

Overflaten av en pyramide er summen av alle sidenes areal.

Test deg selv

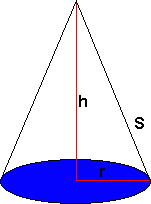
Kjegle

Volum:

<tex>V = \frac{1}{3}\pi r^2h </tex>

Eksempel

En kjegle har en grunnflate med radius 5cm. Høyden i kjeglen er 12 cm. Hva er volumet av kjeglen?

<tex>V = \frac{1}{3}\pi r^2h = \frac 13 \pi (5cm)^2 \cdot 12cm = 314 cm^3</tex>

Eksempel

En kjegle med volum <tex>400cm^3</tex> har høyden 4cm. Hva er radiusen i kjeglens grunnflate?

<tex>V = \frac{1}{3}\pi r^2h \quad \Rightarrow \quad 400cm^3 = \frac{1}{3}\pi r^2 \cdot 4cm \quad \Rightarrow \quad

r^2 = \frac{3 \cdot 400cm^3}{4cm}\quad \Rightarrow \quad r= 17,3 cm </tex>

Eksempel

En kjegle har en grunnflate med radius 6cm og et volum på <tex>300cm^3</tex>. Hva er kjeglens høyde?

<tex>V= \frac 13 \pi r^2h \Rightarrow h = \frac{3V}{\pi r^2} \Rightarrow h =\frac{3 \cdot 300cm^3}{\pi 36cm^2}= 8cm </tex>

Overflate:

<tex> 0 = \pi r^2 + \pi rs</tex>

s er siden av kjeglen og finnes ved å bruke pytagoras:

<tex> s = \sqrt{h^2 + r^2}</tex>

Eksempel

En kjegle har høyde 4cm og radiusen i grunnflaten er 3 cm. Hva er kjeglens overflate?

Finner først s:

<tex> s = \sqrt{r^2+h^2}= \sqrt{9cm^2+16cm^2} = 5cm </tex>

Overflaten blir da:

<tex> 0 = \pi r^2 + \pi rs = \pi \cdot (3cm)^2 + \pi \cdot 3cm \cdot 5cm = 75,4cm^2</tex>

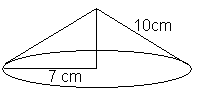
Eksempel

Finn overflatearealet og volumet av kjeglen.

Her kjenner vi S og r og finner høyden h ved å bruke pytagoras:

<tex> h = \sqrt{(10cm)^2 - (7cm)^2}= 7,14cm </tex>

Volumet blir:

<tex>V= \frac 13 \pi r^2h = \frac 13 \pi \cdot (7cm)^2 \cdot 7,14cm = 366 cm^3</tex>

Overflaten blir:

<tex> 0 = \pi r^2 + \pi rs = \pi \cdot (7 cm)^2 + \pi \cdot 7cm \cdot 10 cm = 374cm^2</tex>

Test deg selv

Kule

Volum:

<tex>V = \frac{4}{3}\pi r^3 </tex>

Eksempel

En kule har radius 4 cm. Hva er volumet?

<tex>V = \frac{4}{3}\pi (4cm)^3 = 268,1 cm^3 </tex>

Eksempel

En kule har volum <tex>712cm^3</tex>. Hva er radiusen?

<tex>V = \frac{4}{3}\pi r^3 \\ r = \sqr[3]{\frac{2V}{4 \pi}} \\ r = \sqr[3]{\frac{3 \cdot 268,1 cm^3}{4 \pi}} = 4</tex>

Overflate:

<tex>O = 4 \pi r^2 </tex>

Eksempel

En kule har radius 6 cm. Hva er overflaten?

<tex>O = 4 \pi r^2 = 4 \pi (6cm)^2 = 452,4 cm^2 </tex>

Eksempel

En kule har overflate <tex>400cm^2</tex>. Hva er diameteren?

<tex> O = 4 \pi r^2 \\ r= sqrt{ \frac{O}{4 \pi}} \\ r= sqrt{ \frac{400 cm^2}{4 \pi}}= 5,64</tex>

d = 2r = 11,3 cm.

Test deg selv

---

Tilbake til Ungdomstrinn Hovedside

Tilbake til hovedside