Vektorprodukt: Forskjell mellom sideversjoner
| Linje 67: | Linje 67: | ||
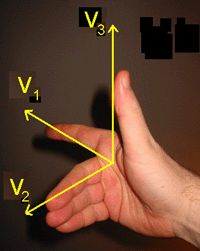
Vi har vektoren | Vi har vektoren <tex> v_1</tex> og vektoren <tex> v_2</tex>. Vektorproduktet av de to vektorene vil være en vektor <tex>v_3</tex> som står vinkelrett på planet som inneholder vektoren <tex>v_1</tex> og vektoren <tex>v_2</tex>. | ||
Dersom du bruker høyre hånd og holder pekefingren parallell med v1, bøy langfingren slik at den er parallell med v2 og la tommelfingren stå rett ut fra hånden. Tommelen peker nå i samme retning som v3. Regelen kalles høyrehåndsregelen. | Dersom du bruker høyre hånd og holder pekefingren parallell med v1, bøy langfingren slik at den er parallell med v2 og la tommelfingren stå rett ut fra hånden. Tommelen peker nå i samme retning som v3. Regelen kalles høyrehåndsregelen. | ||
[[Bilde:Haand.gif]] | |||
| Linje 87: | Linje 87: | ||
Dersom to vektorer i rommet har koordinatene: [x1,y1,z1] og [x2,y2,z2] er vektorproduktet | Dersom to vektorer i rommet har koordinatene: [x1,y1,z1] og [x2,y2,z2] er vektorproduktet | ||
[x1,y1,z1] x [x2,y2,z2] = [y1z2- z1y2, z1x2- x1z2, x1y2-y1x2] | [x1,y1,z1] x [x2,y2,z2] = [y1z2- z1y2, z1x2- x1z2, x1y2-y1x2] | ||
== Bruksområder == | == Bruksområder == | ||
Sideversjonen fra 4. aug. 2011 kl. 17:01
Vektorproduktet er en operasjon mellom to 3-dimensjonale vektorer som har nyttige anvendelser i blant annet areal- og volumberegninger og når vi skal finne normalvektorer til flater og plan i rommet. Merk at vektorproduktet slik det er definert ikke gir mening for annet enn 3- og 7-dimensjonale vektorer, der vi kun har fokus på det 3-dimensjonale tilfellet.
Definisjon av vektorprodukt (kryssprodukt)
Vi bruker notasjonen <tex>\times</tex> for vektorprodukt. Lar vi <tex>\vec{v_1}=(x_1,y_1,z_1)</tex> og <tex>\vec{v_2}=(x_2,y_2,z_2)</tex> er
- <tex>\vec{v_1}\times \vec{v_2}=\left ( y_1z_2-y_2z_1,-(x_1z_2-x_2z_1),x_1y_2-x_2y_1 \right )</tex>
Definisjonen kan også skrives som en determinant som gjør den lettere å huske,
- <tex> \vec{v_1}\times\vec{v_2} = \left| \begin{array}{ccc}i & j & k \\x_1 & y_1 & z_1 \\x_2 & y_2 & z_2 \end{array} \right |</tex>
Utvikler vi i første rad ser vi at determinanten blir
- <tex>\vec{v_1}\times\vec{v_2}= (y_1z_2-y_2z_1)i-(x_1z_2-x_2z_1)j+(x_1y_2-x_2y_1)k</tex>.
Her tolker vi <tex>i,j,k</tex> som enhetsvektorer langs x-,y- og z-aksen, og da ser vi at dette er i overensstemmelse med den første definisjonen.
Merk at kryssproduktet ikke er kommutativt. Bruker vi definisjonen ser vi at
- <tex>\vec{v_2}\times \vec{v_1}=-\vec{v_1}\times \vec{v_2}</tex>
Geometrisk tolkning
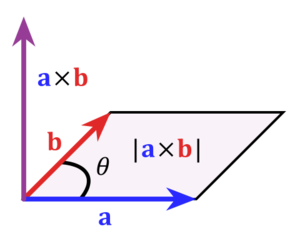
Vektorproduktet <tex>\vec{v_1}\times \vec{v_2}</tex> er en ny vektor, si <tex>\vec{v_3}</tex>, som står normalt (vinkelrett) på både <tex>\vec{v_1}</tex> og <tex>\vec{v_2}</tex> og har lengde <tex>|\vec{v_1}||\vec{v_2}|\sin(\theta)</tex> der <tex>\theta</tex> er den minste vinkelen mellom vektorene. Retningen til <tex>\vec{v_3}</tex> følger høyrehåndsregelen, dvs. at dersom vi tilpasser et slags koordinatsystem slik at <tex>\vec{v_1}</tex> følger x-aksen i positiv retning og <tex>\vec{v_2}</tex> følger y-aksen i positiv retning, vil <tex>\vec{v_3} </tex> peke i positiv retning langs z-aksen.
Absoluttverdien av vektorproduktet
Absoluttverdien
- <tex>|\vec{v_1}\times \vec{v_2}|</tex>
er arealet til parallellogrammet utspent av vektorene. Bruker vi definisjonen kan vi vise at
- <tex>|\vec{v_1}\times \vec{v_2}|=|\vec{v_1}||\vec{v_2}|\sin(\theta)</tex>
der <tex>\theta</tex> er (den minste) vinkelen mellom vektorene. Da ser vi geometrisk at dette er likt arealet av parallellogrammet. For spesialtilfellet <tex>\theta=\frac{\pi}{2}</tex> vil vektorene utspenne et rektangel, og da ser vi enkelt at arealtolkningen stemmer siden <tex>\sin(\frac{\pi}{2})=1</tex>.
Eksempler
Beregning av vektorprodukt
Gitt vektorene <tex>\vec{p}=(1,4,2)</tex> og <tex>\vec{q}=(9,7,1)</tex> beregner vi vektorproduktet som følger:
- <tex> \vec{p}\times\vec{q}=(1,4,2)\times (9,7,1)=(4\cdot 1-7\cdot 2, -(1\cdot 1-9\cdot 2),1\cdot 7-9\cdot 4)=(-10,17,-29)</tex>
Høyrehåndsregelen
Vi har vektoren <tex> v_1</tex> og vektoren <tex> v_2</tex>. Vektorproduktet av de to vektorene vil være en vektor <tex>v_3</tex> som står vinkelrett på planet som inneholder vektoren <tex>v_1</tex> og vektoren <tex>v_2</tex>.
Dersom du bruker høyre hånd og holder pekefingren parallell med v1, bøy langfingren slik at den er parallell med v2 og la tommelfingren stå rett ut fra hånden. Tommelen peker nå i samme retning som v3. Regelen kalles høyrehåndsregelen.
Vektorproduktet skrives v1x v2 og kalles derfor ofte for kryssproduktet. Operasjoner er ikke kommutativ eller assosiativ. Følgende regneregler gjelder:
• v1 x v2 = -(v2 x v1)
•(v1 + v2) x v3 = (v1 x v3) + (v2 x v3)
•(kv1) x v2 = v1 x (kv2)= k(v1 x v2)
Når man tar skalarproduktet av to vektorer blir resultatet en skalar, eller et tall. Når man tar vektorproduktet blir resultatet en ny vektor. Lengden av denne vektoren er gitt ved:
|v1x v2| = |v1|· |v1|· sin γ, γ Є [0º,180º].
Dersom to vektorer i rommet har koordinatene: [x1,y1,z1] og [x2,y2,z2] er vektorproduktet
[x1,y1,z1] x [x2,y2,z2] = [y1z2- z1y2, z1x2- x1z2, x1y2-y1x2]
Bruksområder
Vektorproduktet brukes til å beskrive fenomener i fysikken og det kan også brukes til å regne ut arealer og volumer, samt til å bestemme et plans normalvektor. Eksempelvis har vi at:
•Volumet av en trekantet pyramide bestemt av vektorene v1, v2 og v3 er gitt ved 1/6 ·|(v1x v2)·v3|
•Volumet av en firkantet pyramide bestemt av vektorene v1, v2 og v3 er gitt ved 1/3 ·|(v1x v2)·v3|
•Volumet av en parallellepiped bestemt av vektorene v1, v2 og v3 er gitt ved |(v1x v2)·v3|
•Et parallellogram utspent av vektorene v1 og v2 har et areal gitt ved |v1 x v2|
•En trekant utspent av vektorene v1 og v2 har et areal gitt ved 1/2·|v1 x v2|