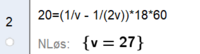1P 2024 høst LK20 LØSNING

Oppgaven som pdf

Diskusjon av oppgaven på matteprat

DEL EN

Oppgave 1

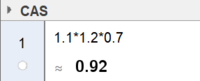
Vare A har en økning på $ \frac{60}{120} = 0,5 = 50$%

Dersom vare B skulle ha en økning på 50%, tilsvarer det 8 kroner. B øker med 10 kroner, altså mer enn 50% og derved prosentvis mer enn vare A.

Oppgave 2

a)

Billiard = tusen millioner millioner = $1 \cdot 10^3 \cdot 10^6 \cdot 10^6 = 1\cdot 10^{3+6+6} = 1 \cdot 10^{15}$

20 billiarder : $20 \cdot 10^{15} = 2,0 \cdot 10^{16}$

b)

Et milligram er et tusendels gram:

$ 7 \cdot 2 \cdot 10^5 \cdot 10^{-3} \cdot 10^{-3} = 14 \cdot 10^{-1} =1,4 kg $

$9 \cdot 3 \cdot 10^5 \cdot 10^{-3} \cdot 10^{-3} = 27 \cdot 10^{-1} = 2,7 kg$

Massen av maur i en vanlig tue vil trolig ligge mellom ca. 1,4 - 2,7 kg.

Oppgave 3

Situasjon A ... Omvendt proporsjonale størrelser. Jo flere som er med jo billigere for den enkelte.

$y = \frac{2200}{x}$ der y er det den enkelte må betale og x er antall betalende.

Situasjon B ... verken proporsjonale eller omvendt proporsjonale størrelser.

Situasjon C ... proporsjonale størrelser. Desto mer vaffelrøre desto mere mel. $Y=kx$

der x er porsjoner vaffelrøre, k er mengde mel til en røre og y er den totale mengde mel.

Oppgave 4

a)

I program 1 kalkuleres en eksponentiell vekst på 4 prosent økning hver måned. I program 2 er veksten lineær, med en økning på 40 enheter per måned.

b)

t forteller hva det totale salget er ved slutten av året, dersom man antar at salget er eksponentielt (program 1) sammenlignet med en lineær vekst (program 2).

Oppgave 5

a)

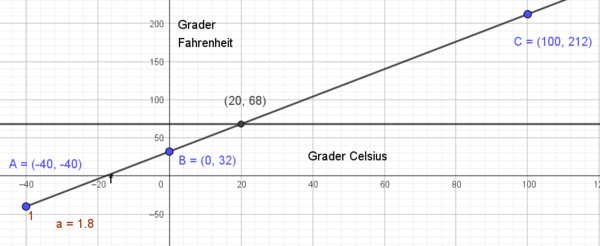
$F = 1,8 C + 32$

Sett inn temperaturen i grader celsius (C), så vil F gi temperaturen i fahrenheit.

b)

Fra figuren i a ser man at 68 Fahrenheit tilsvarer 20 grader Celsius.

DEL TO

Oppgave 1

a)

Abbonenter i 2010:

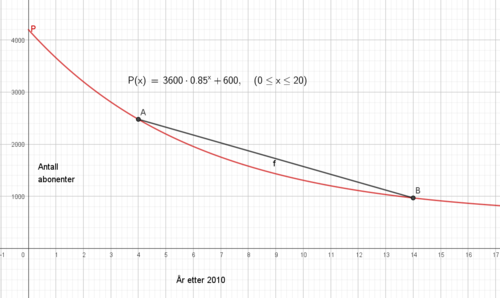
$P(0) = 3600 + 600 = 4200$, eller man kan lese av grafen på y aksen og få samme resultat.

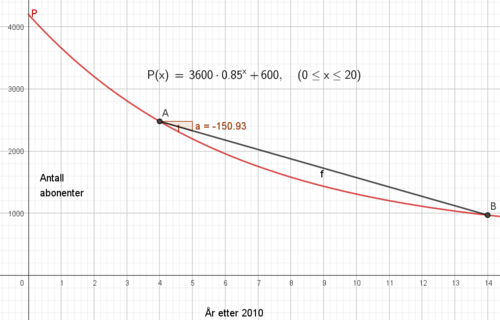
b)

Mellom 2014 og 2024 mister avisen i gjennomsnitt 151 papir abonnenter per år.

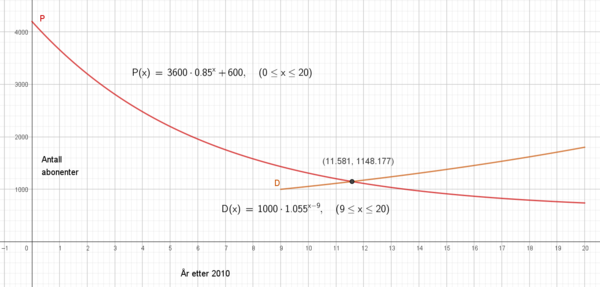
c)

Dersom vi regner origo som 1. januar 2010 vi antall digitalabonnenter passere papirabonnentene på sommeren i 2021.

Oppgave 2

Pasienten skal ha 62,5 ml. i hver dose.

Oppgave 3

Den vil koste mindre enn det den kostet før første prisøkning.

Begrunnelse:

Oppgave 4

a)

Kjøreturen tok ca. 2 minutter lengre tid på mandag.

b)

Hastigheten på de to turene var henholdsvis 27km/h og 54 km/h, i gjennomsnitt.

Kjøreturene tok 20 minutter og 40 minutter.

Oppgave 5

a)

Oppgave 6

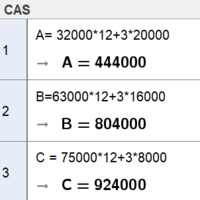
a)

Vi ser at bedrift C gir høyest årslønn med tre reiseoppdrag.

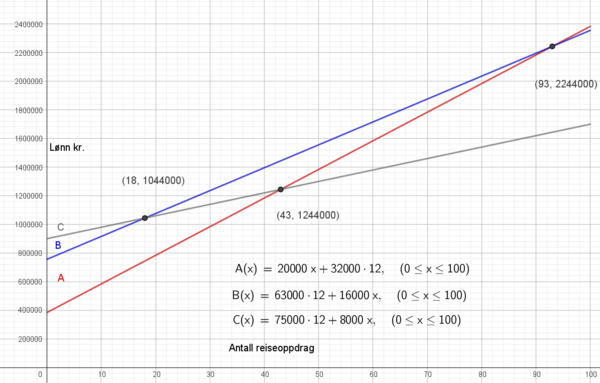
b)

Bedrift C gir høyest lønn ved mindre enn 18 reiseoppdrag. Fra 19 til 92 oppdrag gir firma B høyest lønn. Ved mer enn 93 oppdrag gir firma A høyest årslønn.

Oppgave 8

a)

Dersom hun skjærer som beskrevet blir boksens høyde 1dm. Bredden blir 6dm og lengden 10 dm. Multipliserer vi dette får vi $V = 10 dm \cdot 6 dm \ 1 dm = 60 dm ^3 = 60 liter.$

b)

Her velger jeg å gjøre opg. c først.

c)

Vi kaller sidene i kvadratene som kuttes bort for x. Da blir:

Høyde : $ h = x $

Lengde : $L = 1200-2x$

Bredde: $b = 800-2x$

Volumet blir da:

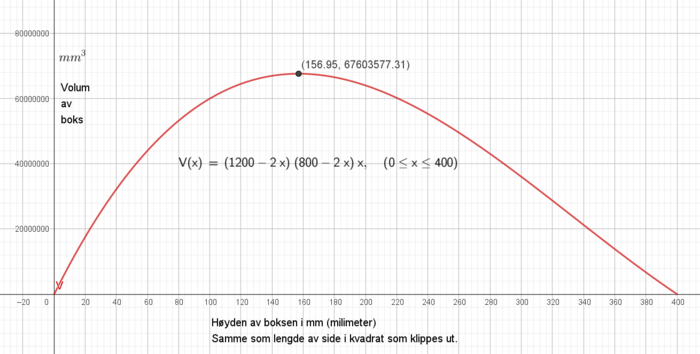
$V(x) = Lbh = (1200 -2x)(800-2x)x = $

d)

Fra figuren i c ser man at vilumet er størs når høyden er 157 mm, det betyr at man må klippe kvadrater med sider på 15,7 cm.

e)

Jo større kvadrater man klipper ut jo høyere blir boksen, samtidig som bunnen i den blir kortere og bredden krymper inn. Når høyden på boksen går mot 400 mm går bredden av biksen mot null. Når bredden er null er volumet null. Gyldighet er derfor fra null til 400 mm.