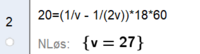1P 2024 høst LK20 LØSNING: Forskjell mellom sideversjoner
| Linje 142: | Linje 142: | ||
====a)==== | ====a)==== | ||
[[File: 22112024-06.png|200px]] | [[File: 22112024-06.png|200px]] | ||
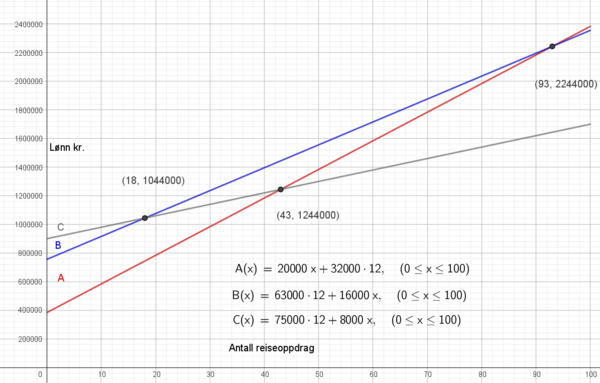
Vi ser at bedrift C gir høyest årslønn med tre reiseoppdrag. | |||
====b)==== | ====b)==== | ||
Sideversjonen fra 23. nov. 2024 kl. 04:51
Diskusjon av oppgaven på matteprat
DEL EN
Oppgave 1
Vare A har en økning på $ \frac{60}{120} = 0,5 = 50$%
Dersom vare B skulle ha en økning på 50%, tilsvarer det 8 kroner. B øker med 10 kroner, altså mer enn 50% og derved prosentvis mer enn vare A.
Oppgave 2
a)
Billiard = tusen millioner millioner = $1 \cdot 10^3 \cdot 10^6 \cdot 10^6 = 1\cdot 10^{3+6+6} = 1 \cdot 10^{15}$
20 billiarder : $20 \cdot 10^{15} = 2,0 \cdot 10^{16}$
b)
Et milligram er et tusendels gram:
$ 7 \cdot 2 \cdot 10^5 \cdot 10^{-3} \cdot 10^{-3} = 14 \cdot 10^{-1} =1,4 kg $
$9 \cdot 3 \cdot 10^5 \cdot 10^{-3} \cdot 10^{-3} = 27 \cdot 10^{-1} = 2,7 kg$
Massen av maur i en vanlig tue vil trolig ligge mellom ca. 1,4 - 2,7 kg.
Oppgave 3
Situasjon A ... Omvendt proporsjonale størrelser. Jo flere som er med jo billigere for den enkelte.
$y = \frac{2200}{x}$ der y er det den enkelte må betale og x er antall betalende.
Situasjon B ... verken proporsjonale eller omvendt proporsjonale størrelser.
Situasjon C ... proporsjonale størrelser. Desto mer vaffelrøre desto mere mel. $Y=kx$
der x er porsjoner vaffelrøre, k er mengde mel til en røre og y er den totale mengde mel.
Oppgave 4
a)
I program 1 kalkuleres en eksponentiell vekst på 4 prosent økning hver måned. I program 2 er veksten lineær, med en økning på 40 enheter per måned.
b)
t forteller hva det totale salget er ved slutten av året, dersom man antar at salget er eksponentielt (program 1) sammenlignet med en lineær vekst (program 2).
Oppgave 5
a)
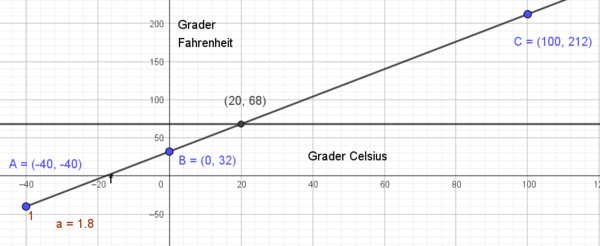
$F = 1,8 C + 32$
Sett inn temperaturen i grader celsius (C), så vil F gi temperaturen i fahrenheit.
b)
Fra figuren i a ser man at 68 Fahrenheit tilsvarer 20 grader Celsius.
DEL TO
Oppgave 1
a)
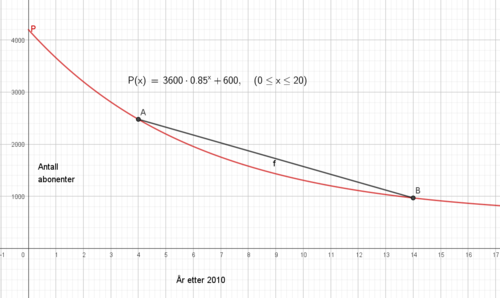
$P(0) = 3600 + 600 = 4200$, eller man kan lese av grafen på y aksen og få samme resultat.
b)
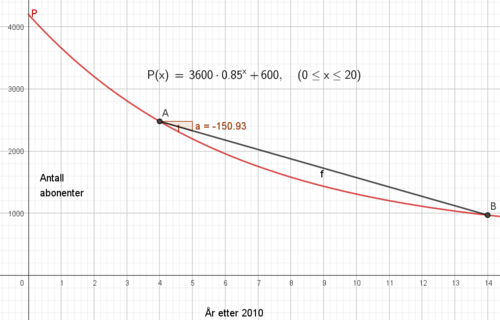
Mellom 2014 og 2024 mister avisen i gjennomsnitt 151 papir abonnenter per år.
c)
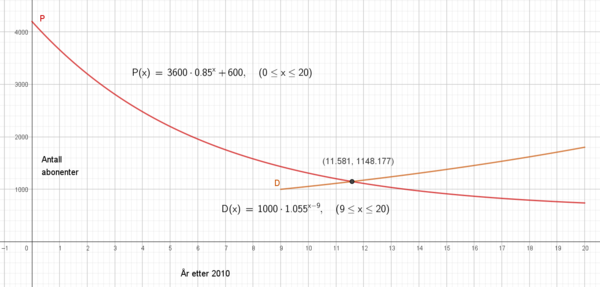
Dersom vi regner origo som 1. januar 2010 vi antall digitalabonnenter passere papirabonnentene på sommeren i 2021.
Oppgave 2
Pasienten skal ha 62,5 ml. i hver dose.
Oppgave 3
Den vil koste mindre enn det den kostet før første prisøkning.
Oppgave 4
a)
Kjøreturen tok ca. 2 minutter lengre tid på mandag.
b)
Hastigheten på de to turene var henholdsvis 27km/h og 54 km/h, i gjennomsnitt.
Kjøreturene tok 20 minutter og 40 minutter.
Oppgave 5
a)
b)
Oppgave 6
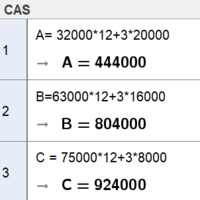
a)
Vi ser at bedrift C gir høyest årslønn med tre reiseoppdrag.