Derivasjon-anvendelser: Forskjell mellom sideversjoner
| Linje 11: | Linje 11: | ||
Eks. 1: | Eks. 1: | ||
Kostnaden ved produksjon av en vare er gitt som: | Kostnaden ved produksjon av en vare er gitt som: | ||
$K(x) = 0,002x^2 + 30x +2000, x \in [ 0, 3000]$ | $K(x) = 0,002x^2 + 30x +2000, x \in [ 0, 3000]$ | ||
Der x er antall enheter. | Der x er antall enheter. | ||
Den deriverte av K(x) er K’(x) = 0,004x + 30 | Den deriverte av K(x) er K’(x) = 0,004x + 30 | ||
Sideversjonen fra 9. jul. 2024 kl. 12:53
Grensekostnader
En kostnadsfunksjon uttrykker hva det koster å produsere x enheter av en vare.
Grensekostnaden forteller hvor mye kostnaden øker dersom man øker produksjonen fra x enheter til x+1 enheter.
Grensekostnaden er tilnærmet lik den deriverte av kostnadsfunksjonen
Eks. 1: Kostnaden ved produksjon av en vare er gitt som:
$K(x) = 0,002x^2 + 30x +2000, x \in [ 0, 3000]$
Der x er antall enheter. Den deriverte av K(x) er K’(x) = 0,004x + 30 Man produseres 500 enheter og ønsker å finne økningen i kostnader når produksjonen økes til 501 enheter: K’(500) = 0,004 · 500 + 30 = 32
Det vil koste ca. 32 kroner å øke produksjonen fra 500 til 501 enheter.
Kostnaden ved å produsere henholdsvis 500 og 5001 enheter er:
K(500) = 0,002 · 500 2 + 30 · 500 + 30 = 15.530kr.
K(501) = 0,002 · 501 2 + 30 · 501 + 30 = 15.562,002kr.
Man ser at nøyaktigheten ved å bruke den deriverte er god. Nøyaktigheten er størst når grafen krummer lite.
Kostnadsfunksjonen er en matematisk modell og vil trolig ikke gi det helt riktige bildet a virkeligheten. Derfor kan man bruke K’(x) når man skal finne grensekostnaden. Feilen er liten og regningen enklere.
Grenseinntekter
Dersom inntekten ved salg av et produkt er I(x) der x er solgte enheter er grenseinntekten I’(x). Grenseinntekten forteller hvor mye inntektene øker når salget øker fra x til x+1 enheter.
Overskudd
En virksomhets overskudd er inntekter minus kostnader.
O(x) = I(x) – K(x)
Overskuddet er størst når O’(x) = 0,
vi får:
O’(x) = I’(x) – K’(x)
O’(x) = 0
I’(x) – K’(x) = 0
I’(x) = K’(x)
Når grensekostnadene er lik grenseinntektene er overskuddet størst.
Eks. 2:
En bedrift har muligheten til å produsere 3000 enheter av et produkt. Hvor mange enheter må produseres for å maksimalisere overskuddet?
x [ 0, 3000]
Kostnadsfunksjonen er gitt som: K(x) = 0,002x2 + 30x +2000
K’(x) = 0,004x + 30
Inntektsfunksjonen er gitt som: I(x) = 0,0001x 2 + 40x
I’(x) = 0,0002x + 40
K’(x) = I’(x)
0,004x + 30 = 0,0002x + 40
x = 2632
Bedriften får størst overskudd ved å produsere 2632 enheter.
Maksimums og minimums problemer
Derivasjon er et egnet verktøy når man arbeider med maksimering eller minimering fordi den deriverte til funksjonen er null i et maksimumspunktet og minimumspunktet til funksjonen.
f’(x) = 0
gir deg alltid x verdien i et maksimums eller minimumspunkt, dersom de finnes.
Eks. 1
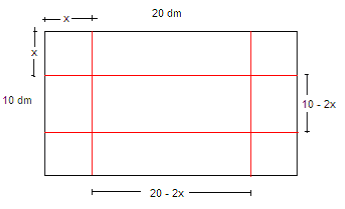
Du har en aluminiumsplate på en ganger to meter og ønsker å forme den til en boks med størst mulig volum.
Volumet av boksen er:
V(x) = bhl = x(20-2x)(10-2x) = x(200 – 40x – 20x +4x 2) = 4x 3 – 60x 2 +200x
V’(x) = 12x 2 – 120x +200
Setter den deriverte lik null:
V’(x) = 0
12x 2 – 120x + 200 = 0
x = 2,1 (tolkning av svarene fører til at vi forkaster den andre muligheten)
Det betyr at boksen får et størst volum dersom den har en høyde på 21 cm.
Eks. 2
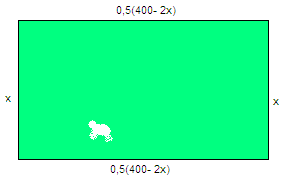
En bonde har en sau og 400 meter gjerde. Hun lurer på hvordan hun kan få det største arealet for sauen, ved å lage en innhegning som er firkantet.
Løsning:
Areal:
A(x) = x(200 – x) = 200x – x 2
Den deriverte av arealet:
A’(x) = 200 – 2x
Setter A’(x) = 0 og får
x = 100
Altså er det et kvadrat som gir størst areal.
Strekning, fart og akslerasjon
Et legeme tilbakelegger strekningen s i løpet av tiden t gitt ved s(t)
Legemets fart v er gitt som v(t) = s'(t)
Farten er den deriverte av strekningen.
Legemets akslerasjon a er gitt som a(t) = v'(t) = s(t)
Akslerasjonen er den deriverte av farten, dvs. den dobbelderiverte av strekningen.
Eks. 3:
En partikkel forflytter seg etter s(t) = 3,7t2
Hvor langt forflytter partikkelen seg på 6 sekunder?' s(6) = 3,7 · 62 = 133,2m
Hva er partikkelen fart etter 4 sekunder?
v(t) = s'(t) = 7,4t
v(4) = s'(4) =7,4 · 4 =29,6 m/s
Hvor lang tid tar det før partikkelen beveger seg med 100 m/s?
v(t) = 100 m/s gir 100m/s = 7,4t, t =100/7,4 = ca. 13,5s
Hva er partikkelens akslerasjon? Er akslerasjonen konstant, eller varierer den med tiden?
a(t) = v'(t) = 7,4m/s 2
Man observerer at t ikke inngår i uttrykket for akslerasjonen, hvilket betyr at den er konstant 7,4 m/s 2, gjennom hele tidsforløpet.