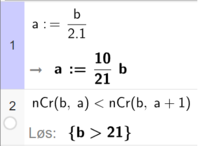S1 2024 Vår LØSNING: Forskjell mellom sideversjoner
| Linje 127: | Linje 127: | ||
===b)=== | ===b)=== | ||
Jeg antar at man kan velge mellom alle siffer fra 0 til 9, altså 10 forskjellige siffer å velge mellom. | |||
Vi har tre ulike typer tegn: små bokstaver, store bokstaver og siffer. Antall måter disse tegntypene kan "stå" på i passordet: | |||
Antall mulige kombinasjoner som følger alle reglene: | |||
Det er altså færre kombinasjoner å velge mellom ved å følge regelsett 2, enn ved å følge regelsett 1. Sikkerheten er derfor muligens dårligere med regelsett 2. | |||
Sideversjonen fra 8. jul. 2024 kl. 16:56
Diskusjon av oppgaven på matteprat
DEL 1
Oppgave 1
Oppgave 2
Setter
Oppgave 3
Oppgave 4
a)
P(2 gule sokker) =
b)
Det er 3*2*1 = 6 måter å trekke 3 sokker med ulik farge: GSH, GHS, HSG, HGS, SGH, SHG. Det er samme sannsynlighet for hver av disse.
P(3 ulike farger) =
P(minst 2 sokker av samme farge) = 1 - P(3 ulike farger) =
Oppgave 5
Vi endrer funksjons definisjonsområde til at 2 ikke er med i definisjonsmengden. :
Vi har ivaretatt alle kravene:
For nærmere forklaring, se s.129-131 i Aschehougs bok "Matematikk S1".
DEL 2
Oppgave 1
a)
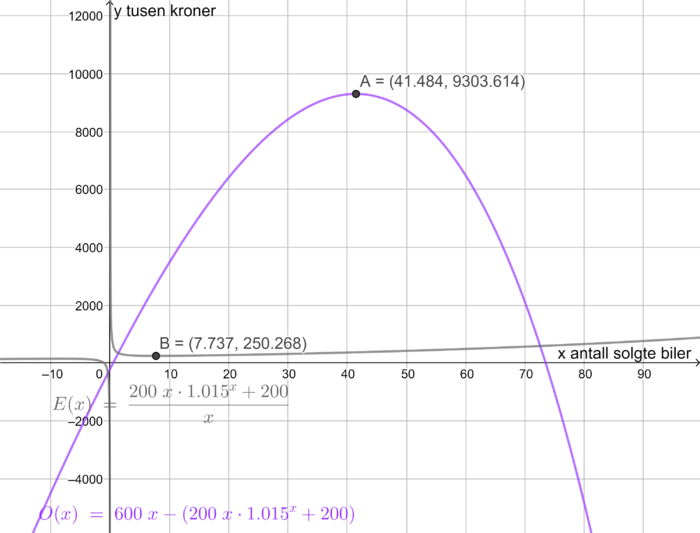
Overskuddsfunksjonen er gitt ved O(x)=I(x)-K(x).
Tegner overskuddsfunksjonen O(x) i Geogebra, og bruker Ekstremalpunkt. Den produksjonsmengden som gir størst overskudd er ca. 41 biler, se punkt A.
b)
Funksjonen for enhetskostnad er gitt ved E(x)=K(x)/x
Tegner funksjonen E(x). Produksjonsmengden som gir lavest mulig enhetskostnad er ca. 8 biler, se punkt B i skjermutklippet i oppgave a).
c)
De avtalte omtrent 784 234 kr per bil i denne kontrakten.
Oppgave 2
a)
b)
Bruker CAS i Geogebra til å teste påstanden for eksempel for
Oppgave 3
a)
Jeg antar at vi bruker det norske alfabetet, som har 29 bokstaver.
Hvis vi regner små og store bokstaver som forskjellige tegn, er det
Antall mulige kombinasjoner hvis vi ikke tar hensyn til at det må være minst én stor og én liten bokstav:
Vi må trekke fra alle kombinasjoner som kun har små bokstaver, og de som kun har store bokstaver.
Antall mulige kombinasjoner som følger alle reglene:
b)
Jeg antar at man kan velge mellom alle siffer fra 0 til 9, altså 10 forskjellige siffer å velge mellom.
Vi har tre ulike typer tegn: små bokstaver, store bokstaver og siffer. Antall måter disse tegntypene kan "stå" på i passordet:
Antall mulige kombinasjoner som følger alle reglene:
Det er altså færre kombinasjoner å velge mellom ved å følge regelsett 2, enn ved å følge regelsett 1. Sikkerheten er derfor muligens dårligere med regelsett 2.