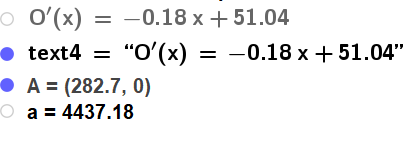1P 2024 vår LK20 LØSNING: Forskjell mellom sideversjoner
| Linje 62: | Linje 62: | ||
=DEL 2= | =DEL 2= | ||
==Oppgave 1== | |||
===a)=== | |||
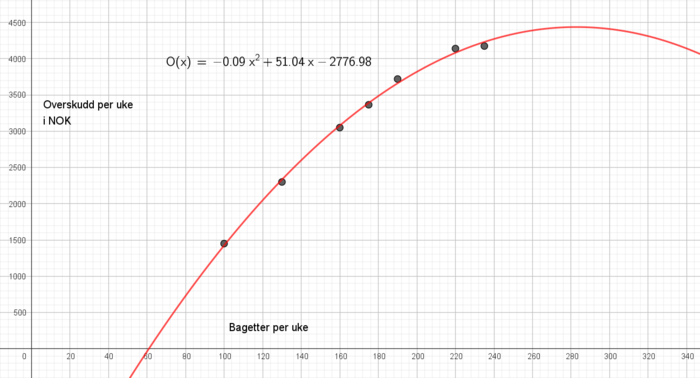
Vi bruker regresjon på Geogebra og får: | |||
[[File:06072024-03.png|700px]] | |||
===b)=== | |||
Dersom man velger å støtte seg på regresjon alene (En modell er mye mer enn bare regresjon) vil kantinen gjøre lurt i å produsere ca. 280 bagetter. | |||
[[File:06072024-04.png]] | |||
''Figuren viser den deriverte av O, A er nullpunktet til den deriverte og a er O(A), altså maksimalt overskudd'' | |||
Det er mange måter å komme fram til gode svar på her. Dersom kantinen produserer 280 bagetter er det ut fra regresjonen sannsynlig at overskuddet ligger et sted mellom 4400 -4500 kroner. Matematikk er en eksakt vitenskap, modellering er ikke det. Det har ingen hensikt å gi eksakte svar med to desimaler. Ved å gi svar som over viser man at man har skjønt at å si noe om fremtiden har elementer av usikkerhet i seg. | |||
===c)=== | |||
==Oppgave 7== | ==Oppgave 7== | ||
Sideversjonen fra 7. jul. 2024 kl. 06:02
Diskusjon av oppgaven på matteprat
DEL 1
Oppgave 1
18 millioner mennesker tilsvarer 2 promille av verdens befolkning.
9 millioner mennesker tilsvarer 1 promille (tusendel) av verdens befolkning.
$9\,000\,000 \cdot 1000 = 9\,000\,000\,000 $
Hele verdens befolkning vil være på 9 milliarder mennesker på det tidspunktet.
Oppgave 2
a)
Tallet 20 000 er hvor mange kroner Ada setter på sparekonto. Tallet 1,0485 er vekstfaktoren for en årlig rente på 4,85 %.
b)
Tallet som blir skrevet ut forteller hvor mange kroner sparebeløpet gjennomsnittlig øker med per år, fra 0 til 10 år.
Oppgave 3
Grafen til f viser sammenhengen mellom to størrelser som er proporsjonale. Dette er fordi grafen til f går gjennom origo, og øker med et konstant stigningstall på 50. Vi kan skrive funksjonsuttrykket til f på formen y = kx, der k er konstant. I dette tilfellet har vi y=50x.
Grafen til p viser sammenhengen mellom to størrelser som er omvendt proporsjonale. Vi kan skrive funksjonsuttrykket til p på formen y = k/x, der k er konstant. For eksempel er y=1000 når x=1, mens y=500 når x=2. Vi har funksjonen y=1000/x.
Oppgave 4
a)
Vi bruker formelen som er gitt i oppgaven. Farten delt på 10 er 7, så vi setter derfor inn 7 for x i formelen.
$B=\frac{x^2}{2}$
$B=\frac{7^2}{2}=\frac{49}{2}=24,5$
Slik kan Viking Redningstjeneste ha regnet ut bremselengden.
b)
Vi skal finne x, så vi gjør om formelen først slik at den er uttrykt ved x.
$B=\frac{x^2}{2}$
$x^2=B\cdot 2$
$x=\sqrt{2B}$
Vi setter inn 40,5 meter for B i formelen og regner ut x:
$x=\sqrt{2\cdot 40,5}=\sqrt{81}=9$
x = 9, det vil si at farten til bilen er 90 km/h.
DEL 2
Oppgave 1
a)
Vi bruker regresjon på Geogebra og får:
b)
Dersom man velger å støtte seg på regresjon alene (En modell er mye mer enn bare regresjon) vil kantinen gjøre lurt i å produsere ca. 280 bagetter.
Figuren viser den deriverte av O, A er nullpunktet til den deriverte og a er O(A), altså maksimalt overskudd
Det er mange måter å komme fram til gode svar på her. Dersom kantinen produserer 280 bagetter er det ut fra regresjonen sannsynlig at overskuddet ligger et sted mellom 4400 -4500 kroner. Matematikk er en eksakt vitenskap, modellering er ikke det. Det har ingen hensikt å gi eksakte svar med to desimaler. Ved å gi svar som over viser man at man har skjønt at å si noe om fremtiden har elementer av usikkerhet i seg.
c)
Oppgave 7
Til sammen kostet alle skoene i utgangspunktet: $800 + 1550 + 1350 = 3700$ kr.
Vennen sine sko utgjorde $\frac{1350}{3700}\cdot 100 = 37$ % av den opprinnelige prisen. Han burde derfor betale 37 % av prisen etter tilbudet.
Med tilbudet blir de billigste skoene gratis, så pris etter tilbud er $1350 + 1550 = 2900$ kr.
Vennen bør betale $0,37\cdot 2900 = 1073$ kr.
Du bør betale $2900 - 1073 = 1827$ kr.