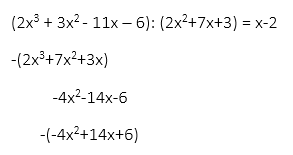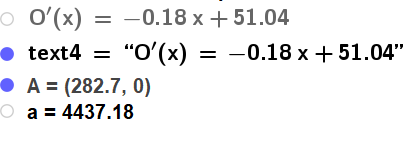1T 2024 vår LK20 LØSNING: Forskjell mellom sideversjoner
| Linje 127: | Linje 127: | ||
==Oppgave 2== | ==Oppgave 2== | ||
[[File:06072024-10.png| | [[File:06072024-10.png|300px]] | ||
===a)=== | ===a)=== | ||
Sideversjonen fra 6. jul. 2024 kl. 15:48
Diskusjon av oppgaven på matteprat
Løsning laget av Sindre Sogge Heggen
Del 1
Oppgave 1
a)
Tangens til vinkelen er definert som motstående katet, delt på hosliggende katet.
$\tan(u) \cdot \tan(v) = \frac{6}{8} \cdot \frac{8}{6} = 1$
Dette betyr at Tom sin påstand er riktig.
b)
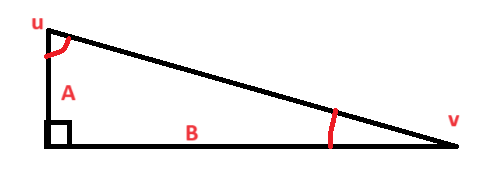
I denne oppgaven skal vi avgjøre om påstanden stemmer for alle rettvinklete trekanter. En generell rettvinklet trekant kan se slik ut:
$tan(u) \cdot tan(v) = \frac{B}{A} \cdot \frac{A}{B} = \frac{A}{A} \cdot \frac{B}{B} = 1$
Påstanden stemmer for alle trekanter av den typen.
Oppgave 2
Dersom P(a) = 0, er P(x) delelig på (x-a)
$P(x) = 2x^3+3x^2-11x-6$
P(0)=-6, P(-1)= 6, P(1)= -12, P(2)= 0. Vi ser også at $P(-3)= -54 + 27 + 33 -6= 0$ Vi observerer at polynomet skifter fortegn mellom P(0) og P(-1). Det kan derfor være fristende å teste om $x=- \frac{1}{2}$ er en rot i polynomet: $P(-\frac 12)= - \frac 14 + \frac 34 + 5,5 - 6 =0$
Røttene er altså $x= -3, x= - \frac 12$ og x = 2.
Polynomet P er da delelig på (x+3), (x + 0,5) og (x-2)
Dersom man deler på (x-2):
Dersom man dividerer tredjegradspolynomet på andregradspolynomet bør man jo få (x-2) som resultat:
Dersom linje tre i oppgaven er riktig må det bety at andregradspolynomet kan faktoriseres. Vi tester: $2x^2+7x+3$ og ser (ved hjelp av koefisientmetoden) at $2x^2+7x+3 = 2((x+3)(x+ \frac 12))$
$P(x) = 2x^3+3x^2-11x-6 = ( 2x^2+7x+3)(x-2) = 2(x-2)(x+ \frac 12)(x + 3)$
Guri KAN ha utført de to divisjonene vist i oppgaven. Faktoriseringen hennes er riktig, men ikke fullstendig.
Oppgave 3
Stort kvadrat minus lite kvadrat:
$a((a-b)+b) - (b\cdot b) = a \cdot a - b \cdot b = a^2-b^2$
Sum av stort rektangel pluss lite rektangel:
$a(a-b) + b(a-b) = a^2-ab +ab - b^2 = a^2-b^2$
Ett eksempel på en identitet, med utgangspunkt i grønt areal er: $a(a-b) + b(a-b) = a^2 - b^2$
Oppgave 4
Det defineres en funksjon som returnerer en andregradsfunksjon. Programmsnutten regner ut den gjennomsnittlige veksten til denne funksjonen mellom 0 og 5 (x verdier)
$ f(x) = x^2-3x+7 $
$v= \frac{f(5)-f(0)}{5} = \frac{17-7}{5} = 2$
Oppgave 5
Generelt: $f(x) = ax^2+bx+c$
Fra figuren leser vi at f(0) =24, dvs c=24
Videre har vi fra figuren at f(-3)= 0 og f(4)= 0 hvilket betyr at (x+3) og (x-4) er faktorer i funksjonen: $(x+3)(x-4) = x^2-x -12$
Vi ser fra konstantleddet c at vi må multiplisere med -2 for å få 24:
$f(x) = -2(x^2-x-12)= -2x^2+2x+24$
DEL TO
Oppgave 1
a)
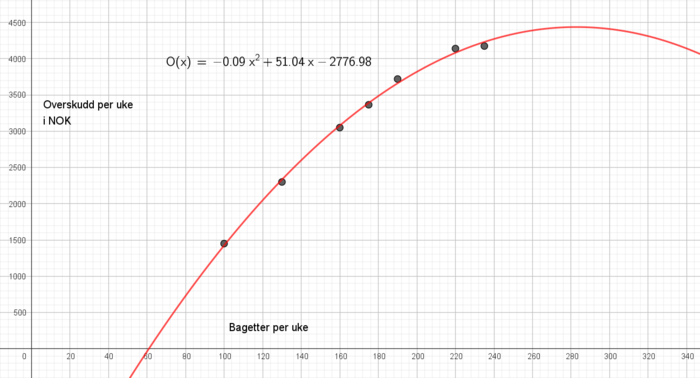
Vi bruker regresjon på Geogebra og får:
b)
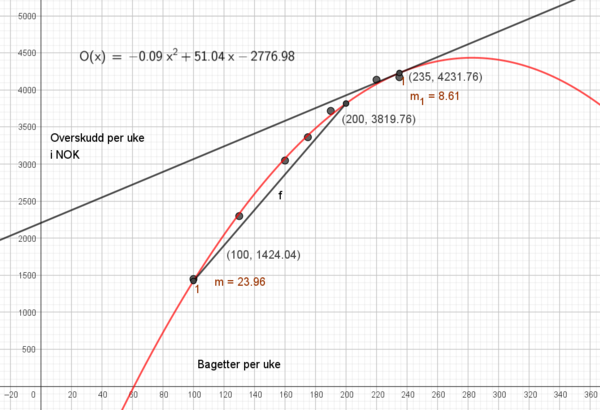
Dersom man velger å støtte seg på regresjon alene (En modell er mye mer enn bare regresjon) vil kantinen gjøre lurt i å produsere ca. 280 bagetter.
Figuren viser den deriverte av O, A er nullpunktet til den deriverte og a er O(A), altså maksimalt overskudd
Det er mange måter å komme fram til gode svar på her. Dersom kantinen produserer 280 bagetter er det ut fra regresjonen sannsynlig at overskuddet ligger et sted mellom 4400 -4500 kroner. Matematikk er en eksakt vitenskap, modellering er ikke det. Det har ingen hensikt å gi eksakte svar med to desimaler. Ved å gi svar som over viser man at man har skjønt at å si noe om fremtiden har elementer av usikkerhet i seg.
c)
Linjen f har stigningstall 23,96. Det betyr at overskuddet øker i gjennomsnitt 24 kroner når bagettsalget økes med en, mellom 100 og 200 bagetter. Legg merke til at økningen er størst rett etter 100 bagetter og så avtar økningen mot 200 bagetter.
d)
Den momentane vekstfarten er 8,61 i (235,f(325)). Det betyr at dersom man øker salget med en bagett, til 236, så øker overskuddet med 8,61 kroner. Se figur i c.
I C laget vi først to punkt, (100, f(100)) og (200, f(200)). Så trakk vi linjestykket mellom dem og fant stigningstallet til linjestykket f. I opg d brukte vi "tangent", og fant stigningstallet til den.
Oppgave 2
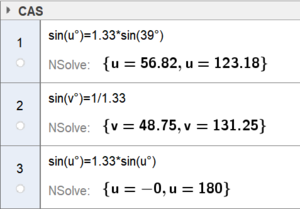
a)
b)
c)
Oppgave 3
Oppgave 4
Oppgave 5
a)
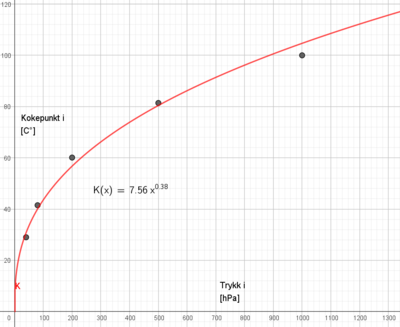
Bruker potensregresjon og får:
b)
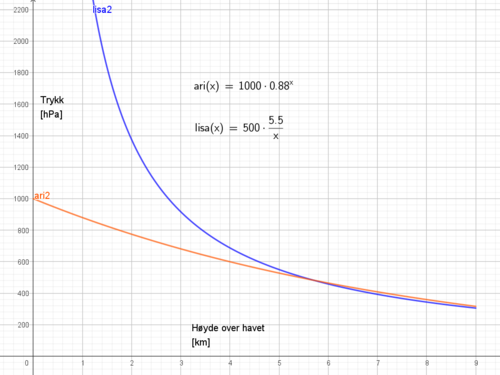
Det er ingen fjell høyere enn 9 km, derfor går derfinisjonsmengden fra null til ni. Vi ser at Lisas modell passer dårlig for lavere fjell, men kan være brukende for fjell over 3000 meter.
c)
Dersom man skal få hardkokte egg må temperaturen (kokepunktet) være over 85 grader, som tilsvarer et trykk på over 600hPa (Figur oppgave a).
Fra figuren i oppgave b ser man at trykket blir lavere enn 600 hPa når høyden overstiger 4000- 4500 meter, avhengig av hvilken modell man bruker. Man bør holde seg på fjell under 4000 meter dersom man er avhengig av hardkokte egg. Alternativt kan man koke dem på forhånd :-)
Oppgave 6
Fra grafen ser man at tangenten i (1,2) har stigningstall -2. P ligger på grafen til f og på tangenten. Da har vi et punkt og et stigningstall, og finner da likningen for den rette linjen:
$y = ax + b \quad$ generelt
$y = -2x +b \quad$ bruker informasjon om stigningstallet
$2 = -2 \cdot 1 + b \quad$ bruker informasjon om punktet for å finne b
b = 4
y = -2x + 4, er likningen for tangenten til f i P.
Oppgave 7
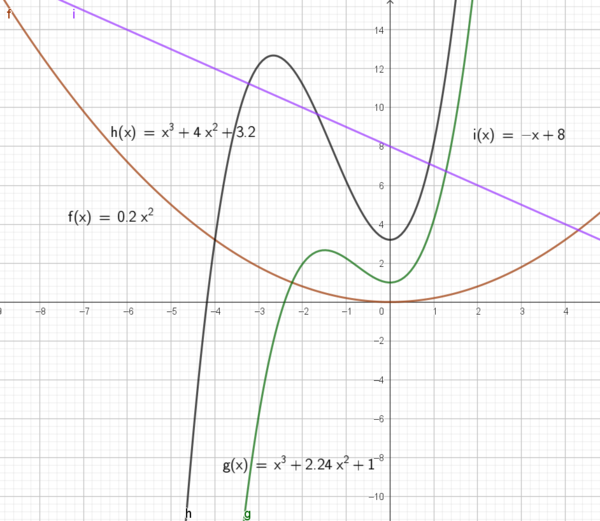
Det er begrenset hvor mye tid man har til utforskning på eksamen, men dette er i alle fall en fin oppgave å ta tak i for å utforske egenskaper ved funksjoner. Bildet over er et første utkast.
- Vi starter med en parabel. En parabel som mangler x leddet er symmetrisk om y aksen. Dersom a i $f(x)= ax^2$ er positiv har funksjonen et minimum. Vår funksjon mangler konstantledd og går gjennom origo. At den mangler konstantledd er ikke noe poeng i seg selv i denne oppgaven. Vi valgte a= 0,2 for å få litt "åpning" på grafen. Parabelen er den brune grafen.
- Den enkleste funksjonen som kan gi en graf tilsvarende den i oppgavesettet, øverst, er en tredjegradsfunksjon. For at den skal ha et bunnpunkt på y- aksen etter ett toppunkt, må koeffisienten foran tredjegradsleddet være positiv. Når funksjonen mangler x ledd vil koeffisienten foran andregradsleddet angi avstanden i x retning til det punkt som har samme funksjonsverdi. (Her er det rom for mye utforskning, langt mer enn hva man har tid til på en eksamen).
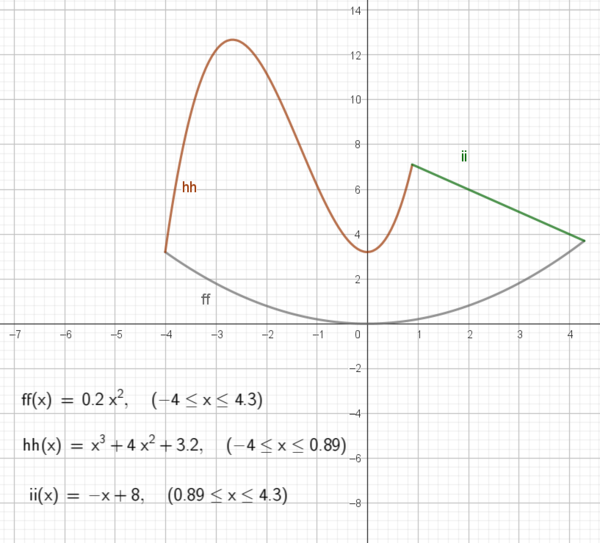
- Til slutt legger man på en rett linje slik at man får en lukket kurve bestående av tre forskjellige funksjoner. Man må definere gyldighetsområdet til hver enkelt funksjon. Denne oppgaven har uendelig mange løsninger. Nedenfor ser du en av dem.