Løsning del 2 10kl Vår 24: Forskjell mellom sideversjoner
| Linje 18: | Linje 18: | ||
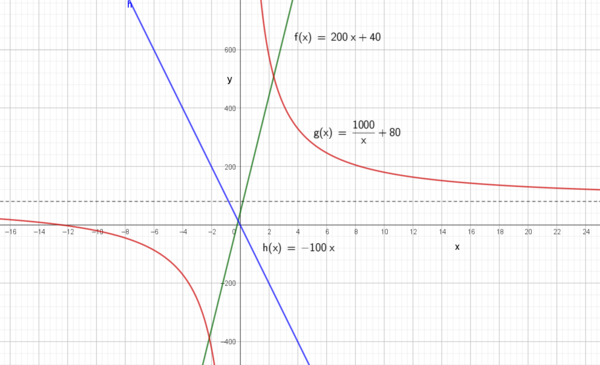
h(x) er også en lineær funksjon. Den mangler konstantledd og går derfor gjennom origo, der y = 0. Den har et negativt stigningstall på 100, derfor avtar den mot høyre med 100 enheter på y aksen, for hver gang x øker med 1. | h(x) er også en lineær funksjon. Den mangler konstantledd og går derfor gjennom origo, der y = 0. Den har et negativt stigningstall på 100, derfor avtar den mot høyre med 100 enheter på y aksen, for hver gang x øker med 1. | ||
g(x) er en brøkfunksjon og grafen er en parabel. Den er ikke definert for null, som er et bruddpunkt. Den nærmere seg y- aksen asymptotisk når x går mot null. Når x går mot uendelig går g mot 80, som er en horisontal asymptote. | |||
===b)=== | ===b)=== | ||
Sideversjonen fra 7. jun. 2024 kl. 14:41
Diskusjon av oppgaven på matteprat
Oppgave 1
Oppgave 2
a)
f(x) er visualisert ved den grønne grafen. Det er en lineær funksjon ( det betyr at grafen er en rett linje), med stigningstall 200 og konstantledd 40. Det vetyr at når x er null, skjærer grafen y-aksen i 40. Stigningstallet forteller at når vi beveger oss en enhet mot
høyre, vokser grafen med 200.
h(x) er også en lineær funksjon. Den mangler konstantledd og går derfor gjennom origo, der y = 0. Den har et negativt stigningstall på 100, derfor avtar den mot høyre med 100 enheter på y aksen, for hver gang x øker med 1.
g(x) er en brøkfunksjon og grafen er en parabel. Den er ikke definert for null, som er et bruddpunkt. Den nærmere seg y- aksen asymptotisk når x går mot null. Når x går mot uendelig går g mot 80, som er en horisontal asymptote.