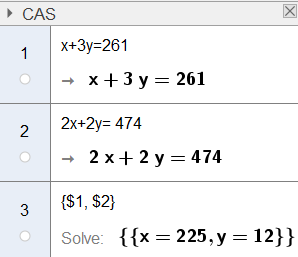2P 2023 Høst LØSNING: Forskjell mellom sideversjoner
| Linje 58: | Linje 58: | ||
===Oppgave 4=== | ===Oppgave 4=== | ||
Dersom man multipliserer (ganger) to tall med hverandre må mist ett av tallene være null, for at produktet skal bli null. Slik er det alltid. | |||
Det som blir sagt om den andre likningen er feil. | |||
$(x+2)(x-3) = -6$ | |||
$x^2-3x+2x-6 +6 =0$ | |||
$x^2-x = 0$ | |||
$x( x-1) =0$ | |||
Her ser man at x=0 eller x=1 er løsninger av likningen. | |||
===DEL TO=== | ===DEL TO=== | ||
Sideversjonen fra 1. des. 2023 kl. 10:00
Diskusjon av oppgaven på matteprat
MAT 1023
DEL EN
Oppgave 1
a)
$415:25= 16,6$ Dvs. man må reise 17 ganger eller mer for at det skal lønne seg.
b)
$\frac{85 \cdot 100}{500} = \frac{85}{5} = 17$ %
Hun sparer 17% på å kjøpe et flexikort.
Oppgave 2
$\frac{40 cm}{2000000 cm} = \frac{4 cm}{200000 cm} = \frac{1}{50000}$
Målestokken er 1: 50 000.
Oppgave 3
Alternativ 1:
Siden median er 8 og typetall 5 tenker jeg
5, 5, 5, 5, 8, 8 .........
Jeg vet at gjennomsnittet skal bli 9 km. på 10 gager blir det 90 km. Jeg mangler 90 - ( 5+5+5+5+8+8) = 54. En mulig løsning blir da:
5, 5, 5, 5, 8, 8, 13, 13, 14, 14
Alternativ 2:
Jeg velger å ta med kun to femmere og tenker at jeg prøver med følgende:
4, 5, 5, 6, 7, 9,...........
Medianverdien vil nå bli 8, selv om jeg ikke bruker 8. Typetallet er 5. Summen skal fortsatt være 90: Plukker ut tall jeg ikke brukte i alternativ 1.
4, 5, 5, 6, 7, 9, 10, 11, 12, 21
Alle krav oppfylt.
Oppgave 4
Dersom man multipliserer (ganger) to tall med hverandre må mist ett av tallene være null, for at produktet skal bli null. Slik er det alltid.
Det som blir sagt om den andre likningen er feil.
$(x+2)(x-3) = -6$
$x^2-3x+2x-6 +6 =0$
$x^2-x = 0$
$x( x-1) =0$
Her ser man at x=0 eller x=1 er løsninger av likningen.
DEL TO
Oppgave 1
x er prisen på en vase, og y er prisen på en rose.
Rosen koster 12 kroner og en vase koster 225 kroner.
Oppgave 2
Oppgave 3
Oppgave 4
Oppgave 5
Oppgave 6
Oppgave 7
Oppgave 8
a)