1P 2023 høst LK20 LØSNING

Oppgave 1

$ 30 mL/kg \cdot 70 kg = 2100 mL = 2,1 L$

Han må drikke 2,1 liter vann per døgn.

Oppgave 2

Ja, 88% $\approx$ 90% $= \frac{90}{100} = \frac {9}{10} $ så det har SSB belegg for å si.

Økningen var fra 80% til 88%, dvs. $\frac{8}{80} = 0,1$, altså 10%

Oppgave 3

U = RI eller $I = \frac{1}{R} \cdot U = \frac UR$

Fra sammenhengen over ser man at når U øker vil I øke.

Dersom motstanden øker vil strømmen minke.

1 er riktig og 2 er feil.

Oppgave 4

a)

Han har trolig sett at det stemmer godt for hele år, fra ett år og oppover. Modellen passer ikke det første leveåret.

b)

Proporsjonale størrelser er på formen y = kx. Her er x og y proporsjonale. Det er ingen konstantledde i proporsjonale størrelser når x = 0 er y også det. Slik er det ikke med H og x. Disse er derfor ikke proporsjonale.

Oppgave 5

$(490000 \cdot 0,80) \cdot 0,86 = $

Tenker at stykket over er en grei løsning, men dersom man ønsker å multiplisere ut vekstfaktorene kan man det:

$490000 \cdot 0,688 =$

DEL TO

Oppgave 1

a)

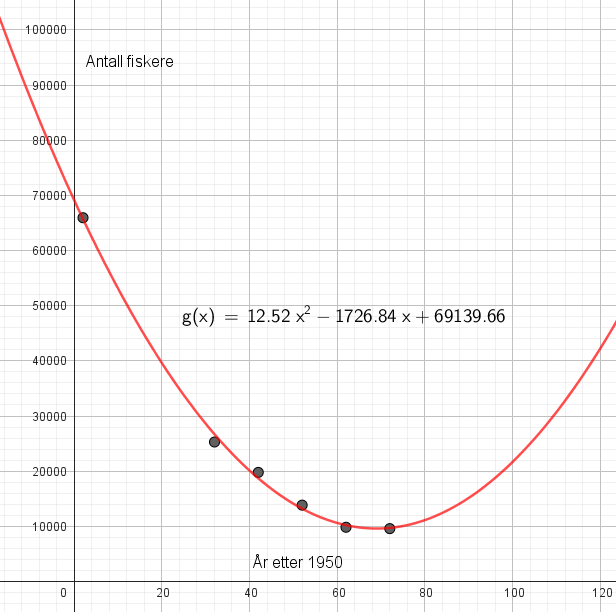
Modellen uttrykt ved g passer godt til å si noe om antall fiskere i tidsperioden (interpolering) men er trolig ikke realistisk i tiden framover.

b)

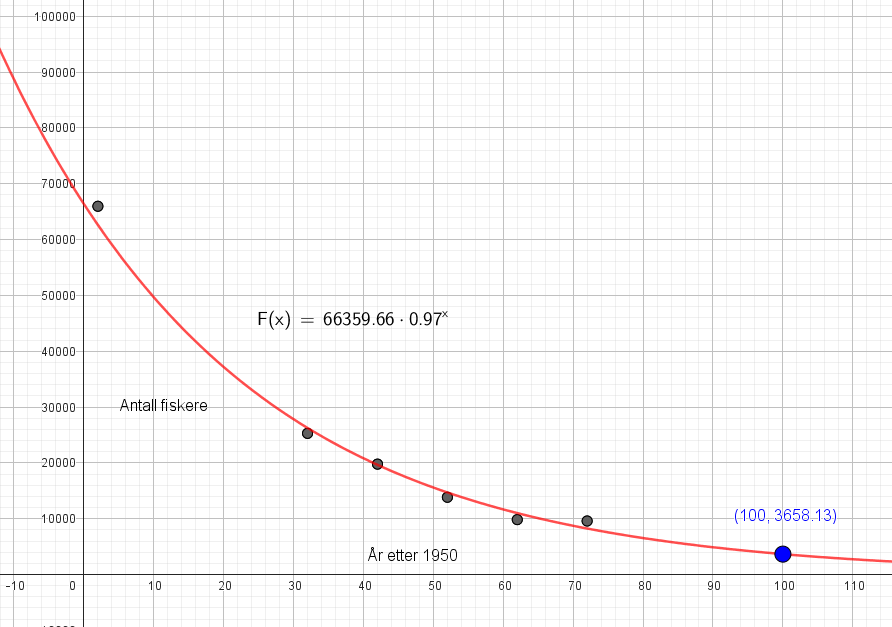
I følge modell F er det i overkant av 3600 fiskere i 2050. F er trolig mer realistisk modell en g. for fremtidig utvikling, selv om g har en bedre tilnærming i målområdet. Med tanke på klimaendringer, AI og politikernes varierende evne til styring er det vanskelig å anslå et fremtidig antall fiskere basert på historiske målinger.

c)

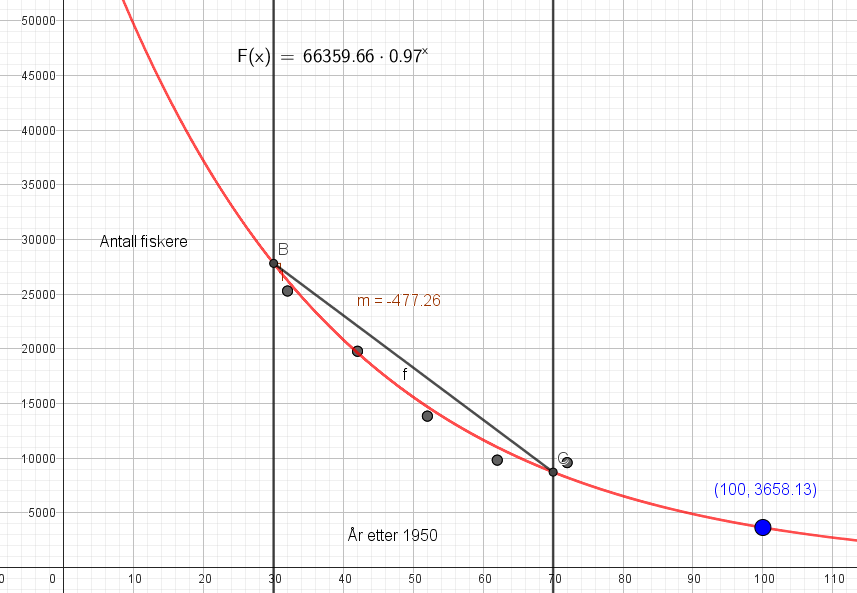
Fra 1980 til 2020 forsvant det i gjennomsnitt ca. 480 fiskere fra yrket hvert eneste år.

Oppgave 2

Arealet av området er: $Areal = L \cdot B$

Areal etter endring: $Nytt_Areal = 1,1 L \cdot 0.8 B = 0,88 LB $

Det nye arealet bli 12% mindre i tillegg til at det blir lengre og smalere.

Oppgave3

a)

Det er $60 \cdot 60 \cdot 24 \cdot 365= 31 536 000$

Vi spiser 500 000 000 : 31536000 = 15,85

Vi spiser ca. 16 pølser i sekundet.

b)

$\frac{13}{500} = 0,026$. Det er 2,6%

Oppgave 4

$1,2mg \cdot 200 = 240mg$

Hunden har fått i seg 240 mg av stoffet. Dersom hunden er under 12 kg bør veterinær kontaktes.

a)

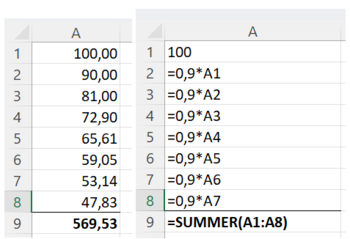
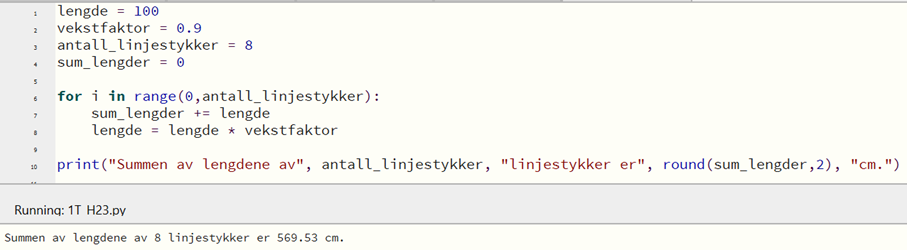
Bruker Excel til å finne lengden på de 8 første linjestykkene, og summerer deretter lengden på disse linjestykkene.

Summen av lengden av de 8 første linjestykkene er 569,5 cm.

b)

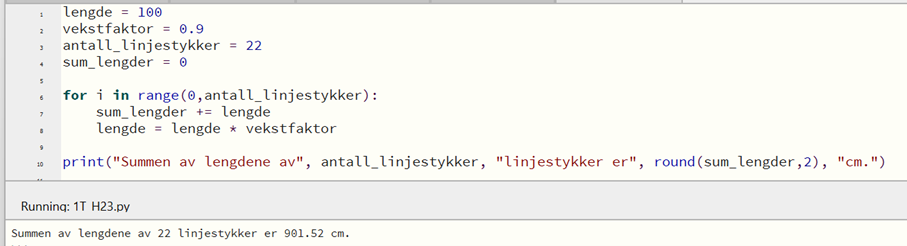
Jeg viser her programmering i Python, hvor jeg kan angi antall linjestykker selv:

For å finne hvor mange linjestykker figuren må ha, for at summen av lengdene skal være minst 9 meter (900 cm), kan jeg prøve meg frem med antall linjestykker i programmet. Jeg finner at 22 linjestykker gir en sum på over 900 cm.

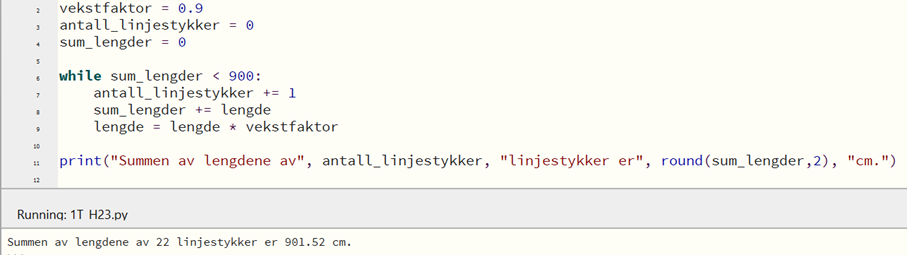
En bedre metode, hvor jeg ikke må prøve meg frem, er å bruke en while-løkke i stedet:

c)

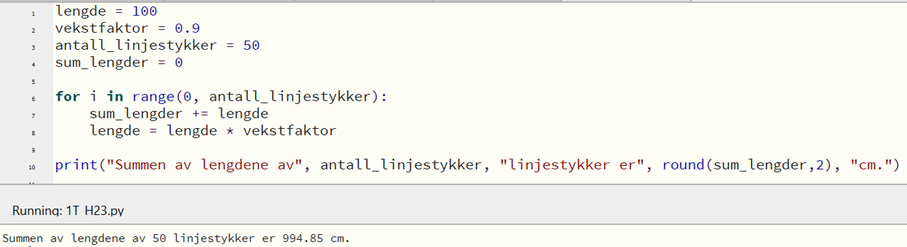
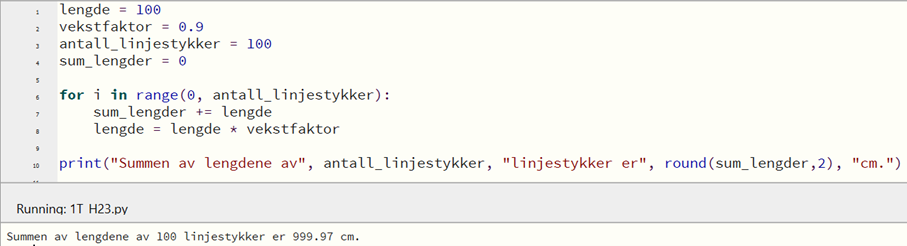
Bruker det første programmet mitt til å regne ut summen av lengdene til henholdsvis 50 og 100 linjestykker.

Regner ut hvor mange prosent forskjell det er for summen av lengdene:

$\frac{999,97 – 994,85}{994,85} \cdot 100 \% = 0,51 \% $

Det er ca. 0,51 % økning i summen av lengdene, dersom vi øker antall linjestykker i figuren fra 50 til 100.

Oppgave 8

Bilen kjører fort på langsidene, men må redusere farten i svingene. Desto krappere sving, desto lavere hastighet (bør ta med at dette er vår antagelse). Vi ser fra grafen at det er tre reduksjoner av hastighet, altså tre svinger. Det ekskluderer bane A, C og F. I bane E er alle svingene like skarpe, da burde hastigheten være lik i alle svingene, så vi ekskluderer E. Det samme argumentet kan brukes om F.

Da står vi igjen med bane B som passer godt til vørt resonnement: Først en halv langside med høy fart, så en skarp sving med lav fart. Etter en ny langside en enda skarpere sving, med enda lavere fart. Den siste svingen er ikke så krapp, og farten heller ikke så lav. Bane B er riktig bane.